题目内容
设函数f(x)=a2x+2ax-1,其中a>0且a≠1.
(1)若a=
,请用定义证明f(x)在R上单调递增;
(2)若函数f(x)在区间[-1,1]上的最大值为14,求a的值.
(1)若a=
| 1 |
| 2 |
(2)若函数f(x)在区间[-1,1]上的最大值为14,求a的值.
考点:函数单调性的判断与证明,二次函数在闭区间上的最值
专题:计算题,函数的性质及应用
分析:(1)设x1<x2,证明f(x2)-f(x1)>0即可.
(2)先ax=t,将函数转化成关于t的二次函数,注意讨论a的大小,求出变量t的范围,结合开口方向和对称轴求出最大值,建立等量关系,解之即可.
(2)先ax=t,将函数转化成关于t的二次函数,注意讨论a的大小,求出变量t的范围,结合开口方向和对称轴求出最大值,建立等量关系,解之即可.
解答:
解:(1)设x1<x2,则
f(x2)-f(x1)=(
)2x2+2(
)x2-1-((
)2x1+2(
)x1-1)=(
)2x2-(
)2x1+2(
)x2-2(
)x1
∵2x2>2x1,函数g(x)=(
)x在定义域内单调递减.
∴(
)2x2-(
)2x1>0,2(
)x2-2(
)x1>0即有f(x2)-f(x1)>0.
故f(x)在R上单调递增.
(2)设ax=t,则y=f(t)=t2+2t-1=(t+1)2-2
其对称轴是t=-1,若a>1,x∈[-1,1]时,t∈[
,a]
二次函数y=f(t)在[
,a]上是增函数,从而ymax=f(a)=a2+2a-1
令a2+2a-1=14,得a=3(a=-5舍去)
若0<a<1,x∈[-1,1]时t∈[a,
],y=f(t)在[a,
]上仍是增函数,
从而ymax=f(
)=
+
-1=14,解得a=
或a=-
(舍去)
综合得:a=3或a=
.
f(x2)-f(x1)=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵2x2>2x1,函数g(x)=(
| 1 |
| 2 |
∴(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故f(x)在R上单调递增.
(2)设ax=t,则y=f(t)=t2+2t-1=(t+1)2-2
其对称轴是t=-1,若a>1,x∈[-1,1]时,t∈[
| 1 |
| a |
二次函数y=f(t)在[
| 1 |
| a |
令a2+2a-1=14,得a=3(a=-5舍去)
若0<a<1,x∈[-1,1]时t∈[a,
| 1 |
| a |
| 1 |
| a |
从而ymax=f(
| 1 |
| a |
| 1 |
| a2 |
| 2 |
| a |
| 1 |
| 3 |
| 1 |
| 5 |
综合得:a=3或a=
| 1 |
| 3 |
点评:本题主要考查了函数的最值及其几何意义,以及指数函数的单调性与特殊点,考察了函数单调性的判断与证明,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
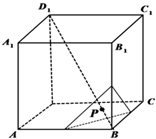 如图,正方体ABCD-A1B1C1D1的棱长为
如图,正方体ABCD-A1B1C1D1的棱长为| 3 |
| 1 |
| 2 |
| 5 |
| 2 |
A、[
| ||||||
B、[
| ||||||
C、[
| ||||||
D、[
|
从正方体ABCD-A1B1C1D1的6个表面中选取3个面,其中有2个面不相邻的选法共有( )
| A、8种 | B、12种 |
| C、16种 | D、20种 |