题目内容
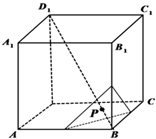 如图,正方体ABCD-A1B1C1D1的棱长为
如图,正方体ABCD-A1B1C1D1的棱长为| 3 |
| 1 |
| 2 |
| 5 |
| 2 |
A、[
| ||||||
B、[
| ||||||
C、[
| ||||||
D、[
|
考点:棱柱的结构特征
专题:函数的性质及应用,空间位置关系与距离
分析:验证x=BP=
,1,
时,y=f(x)的值是什么,分析函数y=f(x)的变化情况,从而得出正确的判断.
| 1 |
| 2 |
| 3 |
| 2 |
解答:
解:∵正方体ABCD-A1B1C1D1的棱长为
,
∴BD1=
AB=3,
当BP=
时,如图所示;
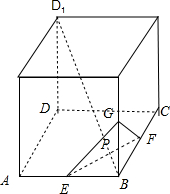
三棱锥B-EFG的底面是正三角形,设边长EF=a,则BE=
,
∴
•
a2•
=
•
•
•
•
;
解得a=
,
y=f(x)=
;
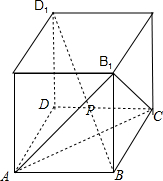
当EF=
AB=
时,y=f(x)=3
,如图所示;
•
•
•
•BP=
•
•
•
•
,
此时BP=1;
当BP=
时,截面为六边形EFGHIJ,
且EF=FG=GH=HI=IJ=JE=
AC=
,如图所示;
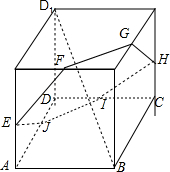
此时y=f(x)=
;
∴x∈[
,
]时,函数y=f(x)的值域应为[
,3
].
故选:B.
| 3 |
∴BD1=
| 3 |
当BP=
| 1 |
| 2 |

三棱锥B-EFG的底面是正三角形,设边长EF=a,则BE=
| a | ||
|
∴
| 1 |
| 3 |
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| a | ||
|
| a | ||
|
| a | ||
|
解得a=
| ||
| 2 |
y=f(x)=
3
| ||
| 2 |
当EF=
| 2 |
| 6 |
| 6 |

| 1 |
| 3 |
| ||
| 4 |
| 6 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
此时BP=1;
当BP=
| 3 |
| 2 |
且EF=FG=GH=HI=IJ=JE=
| 1 |
| 2 |
| ||
| 2 |

此时y=f(x)=
3
| ||
| 2 |
∴x∈[
| 1 |
| 2 |
| 5 |
| 2 |
3
| ||
| 2 |
| 6 |
故选:B.
点评:本题考查了空间几何体的应用问题,也考查了作图和读图的能力,解题时应根据几何体的特征和条件进行分析变化情况,是难题.

练习册系列答案
相关题目
如果如图撑血运行后,输出结果为132,那么程序中UNTIL,后面的条件应为( )


| A、i>11 | B、i≥11 |
| C、i≤11 | D、i<11 |
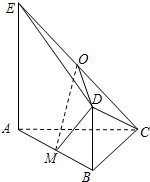 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥AB,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥AB,BD=