题目内容
△ABC中，a，b，c是A，B，C所对的边，S是该三角形的面积，且
=
（1）求∠B的大小；
（2）若a=4，S=5
，求b的值．
| cosB |
| cosC |
| b |
| 2a-c |
（1）求∠B的大小；
（2）若a=4，S=5
| 3 |
考点：余弦定理,正弦定理
专题：解三角形
分析：（1）已知等式利用正弦定理化简，整理后利用两角和与差的正弦函数公式及诱导公式化简，由sinA不为0求出cosB的值，即可确定出B的度数；
（2）利用三角形面积公式列出关系式，把a，S，以及sinB的值代入求出c的值，再利用余弦定理即可求出b的值．
（2）利用三角形面积公式列出关系式，把a，S，以及sinB的值代入求出c的值，再利用余弦定理即可求出b的值．
解答：
解：（1）已知等式利用正弦定理化简得：
=
=
，
∴2sinAcosB-sinCcosB=sinBcosC，
∴2sinAcosB=sin（B+C），
∴2sinAcosB=sinA，
∵sinA≠0，∴cosB=
，
则B=60°；
（2）∵S=
acsinB，a=4，S=5
，
∴c=5，
由余弦定理得：b2=a2+c2-2accosB=16+25-2×4×5×
=21，
则b=
．
| cosB |
| cosC |
| b |
| 2a-c |
| sinB |
| 2sinA-sinC |
∴2sinAcosB-sinCcosB=sinBcosC，
∴2sinAcosB=sin（B+C），
∴2sinAcosB=sinA，
∵sinA≠0，∴cosB=
| 1 |
| 2 |
则B=60°；
（2）∵S=
| 1 |
| 2 |
| 3 |
∴c=5，
由余弦定理得：b2=a2+c2-2accosB=16+25-2×4×5×
| 1 |
| 2 |
则b=
| 21 |
点评：此题考查了正弦、余弦定理，以及三角形面积公式，熟练掌握定理及公式是解本题的关键．
练习册系列答案
相关题目
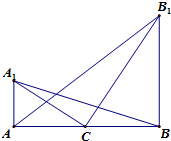如图，在水平地面上有两座直立的相距60m的铁塔AA1和BB1．已知从塔AA1的底部看塔BB1顶部的仰角是从塔BB1的底部看塔AA1顶部的仰角的2倍，从两塔底部连线中点C分别看两塔顶部的仰角互为余角．则从塔BB1的底部看塔AA1顶部的仰角的正切值为如果如图撑血运行后，输出结果为132，那么程序中UNTIL，后面的条件应为（ ）
| A、i＞11 | B、i≥11 |
| C、i≤11 | D、i＜11 |