��Ŀ����
��֪Բ��ΪC��Բ����������������Բ��Cλ��x���������ϣ���ֱ��3x-4y+7=0���У��ұ�y��صõ��ҳ�Ϊ2
��ԲC�����С��13��
��1����ԲC�ı����̣�
��2����ԲC��������M��N����ֱ��x+2y-1=0�Գƣ���|MN|=2
����ֱ��MN�ķ��̣�
��3�������P��0��3����ֱ��l��ԲC���ڲ�ͬ������A��B����OA��OBΪ�ڱ���ƽ���ı���OADB���Ƿ����������ֱ��l��ʹ��ֱ��OD��PCǡ��ƽ�У�������ڣ����l�ķ��̣���������ڣ���˵�����ɣ�
| 3 |
��1����ԲC�ı����̣�
��2����ԲC��������M��N����ֱ��x+2y-1=0�Գƣ���|MN|=2
| 3 |
��3�������P��0��3����ֱ��l��ԲC���ڲ�ͬ������A��B����OA��OBΪ�ڱ���ƽ���ı���OADB���Ƿ����������ֱ��l��ʹ��ֱ��OD��PCǡ��ƽ�У�������ڣ����l�ķ��̣���������ڣ���˵�����ɣ�
���㣺Բ�ı�����,ֱ����Բ��λ�ù�ϵ
ר�⣺�ۺ���,ֱ����Բ
��������1�����õ㵽ֱ�ߵľ��빫ʽ����Ϲ��ɶ������������̣�����ԲC�����С��13��������ԲC�ı����̣�
��2�����ֱ�߷��̣����õ㵽ֱ�ߵľ����Լ������������ֱ�߷����еIJ��������ɵõ�ֱ�߷��̣�
��3���������ۣ����ֱ�߷�����Բ�ķ�������������Τ�ﶨ�����ټ���
��
����-3��x1+x2��=y1+y2�����ɵó����ۣ�
��2�����ֱ�߷��̣����õ㵽ֱ�ߵľ����Լ������������ֱ�߷����еIJ��������ɵõ�ֱ�߷��̣�
��3���������ۣ����ֱ�߷�����Բ�ķ�������������Τ�ﶨ�����ټ���
| OD |
| PC |
���
�⣺��1����ԲC����x-a��2+y2=R2��a��0����
������֪
�����a=1��a=
������3�֣�
�֡�S=��R2��13��
��a=1��
��ԲC�ı�����Ϊ����x-1��2+y2=4�� ����4�֣�
��2�������⣬����ֱ��MN�ķ���Ϊ2x-y+m=0������6�֣�
��Բ��O��ֱ��MN�ľ���d=
��
�ɴ������Ҷ����ã�
+3=4����m=-2��
��
����ֱ��MN�ķ���Ϊ��2x-y-2��
=0������8�֣�
��3����б�ʲ�����ʱ��ֱ��lΪ��x=0���������⣮
��б�ʴ���ʱ����ֱ��l��y=kx+3��A��x1��y1����B��x2��y2����
�֡�l��ԲC�ཻ�ڲ�ͬ�����㣬
ֱ�ߴ���Բ�ķ��̣���ȥy�ã���1+k2��x2+��6k-2��x+6=0������9�֣�
���=��6k-2��2-24��1+k2��=3k2-6k-5��0��
���k��1-
��k��1+
��
x1+x2=-
��y1+y2=k��x1+x2��+6=
��
����
��
����-3��x1+x2��=y1+y2��
��3��
=
��
���k=
������k��1-
��k��1+
�����費������
�����������ֱ��l�� ����13�֣�
������֪
|
| 13 |
| 8 |
�֡�S=��R2��13��
��a=1��
��ԲC�ı�����Ϊ����x-1��2+y2=4�� ����4�֣�
��2�������⣬����ֱ��MN�ķ���Ϊ2x-y+m=0������6�֣�
��Բ��O��ֱ��MN�ľ���d=
| |2+m| | ||
|
�ɴ������Ҷ����ã�
| (2+m)2 |
| 5 |
| 5 |
����ֱ��MN�ķ���Ϊ��2x-y-2��
| 5 |
��3����б�ʲ�����ʱ��ֱ��lΪ��x=0���������⣮
��б�ʴ���ʱ����ֱ��l��y=kx+3��A��x1��y1����B��x2��y2����
�֡�l��ԲC�ཻ�ڲ�ͬ�����㣬
ֱ�ߴ���Բ�ķ��̣���ȥy�ã���1+k2��x2+��6k-2��x+6=0������9�֣�
���=��6k-2��2-24��1+k2��=3k2-6k-5��0��
���k��1-
2
| ||
| 3 |
2
| ||
| 3 |
x1+x2=-
| 6k-2 |
| 1+k2 |
| 2k+6 |
| 1+k2 |
����
| OD |
| PC |
��3��
| 6k-2 |
| 1+k2 |
| 2k+6 |
| 1+k2 |
���k=
| 3 |
| 4 |
2
| ||
| 3 |
2
| ||
| 3 |
�����������ֱ��l�� ����13�֣�
���������⿼��Բ�ķ��̣�����ֱ����Բ��λ�ù�ϵ������Τ�ﶨ�������ã�����ѧ���������������������ۺ���ǿ��

��ϰ��ϵ�д�
 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д� �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�����Ŀ
��ͼ��������ABCD-A1B1C1D1�У�AB1��C1B���ɵĽ�Ϊ��������
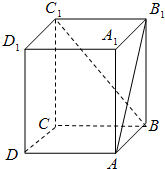

A��
| ||
B��
| ||
C��
| ||
D��
|
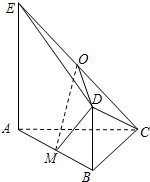 ��ͼ��ƽ��ABDE��ƽ��ABC����ABC�ǵ���ֱ�������Σ�AC=BC=4���ı���ABDE��ֱ�����Σ�BD��AE��BD��AB��BD=
��ͼ��ƽ��ABDE��ƽ��ABC����ABC�ǵ���ֱ�������Σ�AC=BC=4���ı���ABDE��ֱ�����Σ�BD��AE��BD��AB��BD=