题目内容
若2cos2α=sin(α+
),则sin2α= .
| π |
| 4 |
考点:二倍角的正弦,两角和与差的正弦函数
专题:三角函数的求值
分析:由已知化为2(cos2α-sin2α)=
(sinα+cosα),从而得到cosα-sinα的值,两边同时平方可解得sin2α的值.
| ||
| 2 |
解答:
解:∵2cos2α=sin(α+
),
∴可得:2(cos2α-sin2α)=
(sinα+cosα),
∴得cosα-sinα=
,
∴两边同时平方可得:1-sin2α=
,
∴sin2α=
.
故答案为:
.
| π |
| 4 |
∴可得:2(cos2α-sin2α)=
| ||
| 2 |
∴得cosα-sinα=
| ||
| 4 |
∴两边同时平方可得:1-sin2α=
| 1 |
| 8 |
∴sin2α=
| 7 |
| 8 |
故答案为:
| 7 |
| 8 |
点评:本题主要考查了二倍角的正弦公式,两角和与差的正弦函数公式的应用,属于基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知集合P={x|x2-2x-3>0},Q={x|log2(x-2)<1},则(∁RP)∩Q=( )
| A、{x|2<x≤3} |
| B、{x|-1≤x≤3} |
| C、{x|3<x≤4} |
| D、{x|3<x≤4或x<-1} |
曲线y=xn(x∈N)在点P(
,(
)n)处的切线的斜率为20,则n为( )
| 2 |
| 2 |
| A、7 | B、6 | C、5 | D、4 |
已知:α,β是不同的平面,l,m,n是不同的直线,则下列说法正确的是( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
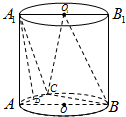 如图,平面ABB1A1为圆柱OO1的轴截面,点C为底面圆周上异于A,B的任意一点.
如图,平面ABB1A1为圆柱OO1的轴截面,点C为底面圆周上异于A,B的任意一点.