题目内容
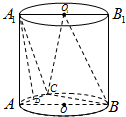 如图,平面ABB1A1为圆柱OO1的轴截面,点C为底面圆周上异于A,B的任意一点.
如图,平面ABB1A1为圆柱OO1的轴截面,点C为底面圆周上异于A,B的任意一点.(Ⅰ)求证:BC⊥平面A1AC;
(Ⅱ)若D为AC的中点,求证:A1D∥平面O1BC.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)只要证明BC垂直于平面A1AC的两条相交直线AC,AA1即可;
(Ⅱ)取BC中点E,连结DE、O1E,只要证明A1D∥EO1,然后利用线面平行的判定定理即可证明结论.
(Ⅱ)取BC中点E,连结DE、O1E,只要证明A1D∥EO1,然后利用线面平行的判定定理即可证明结论.
解答:
证明:(Ⅰ)因为AB为圆O的直径,点C为圆O上的任意一点
∴BC⊥AC …(2分)
又圆柱OO1中,AA1⊥底面圆O,
∴AA1⊥BC,即BC⊥AA1 …(4分)
而AA1∩AC=A
∴BC⊥平面A1AC …(6分)
(Ⅱ)取BC中点E,连结DE、O1E,
∵D为AC的中点
∴△ABC中,DE∥AB,且DE=
AB …(8分)
又圆柱OO1中,A1O1∥AB,且A1O1=
AB
∴DE∥A1O1,DE=A1O1
∴A1DEO1为平行四边形 …(10分)
∴A1D∥EO1 …(11分)
而A1D?平面O1BC,EO1?平面O1BC
∴A1D∥平面O1BC …(12分)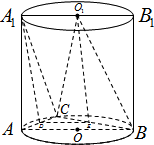
∴BC⊥AC …(2分)
又圆柱OO1中,AA1⊥底面圆O,
∴AA1⊥BC,即BC⊥AA1 …(4分)
而AA1∩AC=A
∴BC⊥平面A1AC …(6分)
(Ⅱ)取BC中点E,连结DE、O1E,
∵D为AC的中点
∴△ABC中,DE∥AB,且DE=
| 1 |
| 2 |
又圆柱OO1中,A1O1∥AB,且A1O1=
| 1 |
| 2 |
∴DE∥A1O1,DE=A1O1
∴A1DEO1为平行四边形 …(10分)
∴A1D∥EO1 …(11分)
而A1D?平面O1BC,EO1?平面O1BC
∴A1D∥平面O1BC …(12分)

点评:本题主要考查直线与直线、直线与平面、平面与平面的位置关系;考查学生的空间想象能力及推理论证能力.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
已知高为1的梯形ABCD内接于半径为1的圆O,若梯形的上底CD=1,则(
+
)•
=( )
| OA |
| OB |
| OC |
| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
空间中有四点A,B,C,D,其中
=(2m,m,2),
=(m,m+1,-5),且
+
=(5,
,-3),则直线AB和CD( )
| AB |
| CD |
| AB |
| CD |
| 13 |
| 3 |
| A、平行 | B、异面 |
| C、必定相交 | D、必定垂直 |
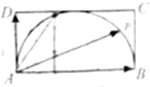 如图,矩形ABCD中,AB=2AD=2,点P在以AB为直径的半圆上移动,若
如图,矩形ABCD中,AB=2AD=2,点P在以AB为直径的半圆上移动,若| AP |
| AB |
| AD |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
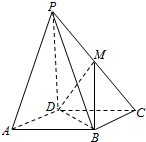 在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是边长为2的正方形,且PD=AB.
在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是边长为2的正方形,且PD=AB.