题目内容
已知数列{an}是等差数列(ak与公差d均不为0).
(1)求证:k取任何正整数,方程akx2+2ak+1x+ak+2=0都有一个相同的实根;
(2)若上述方程的另一非零实根为ak,求证:{
}是等差数列.
(1)求证:k取任何正整数,方程akx2+2ak+1x+ak+2=0都有一个相同的实根;
(2)若上述方程的另一非零实根为ak,求证:{
| 1 |
| 1+an |
考点:等差数列的性质,等差关系的确定
专题:综合题,等差数列与等比数列
分析:(1)依题意,2ak+1=ak+ak+2,于是原方程可转化为(akx+ak+2)(x+1)=0,从而可证结论;
(2)原方程另一根为xn,利用韦达定理,可求得xn=-
=-1-
,继而得
=-
,利用等差数列的定义,证明即可.
(2)原方程另一根为xn,利用韦达定理,可求得xn=-
| ak+2 |
| ak |
| 2d |
| ak |
| 1 |
| 1+xn |
| ak |
| 2d |
解答:
证明:(1)∵数列{an}是等差数列,
∴2ak+1=ak+ak+2,
原方程可转化为(akx+ak+2)(x+1)=0,
∴k取任何正整数,方程akx2+2ak+1x+ak+2=0都有一个相同的实根-1;
(2)由题意,原方程另一根为xn,xn=-
=-1-
,
∴1+xn=-
,
∴
=-
,
∴
-
=
=-
(常数).
∴数列{
}即{
}是以-
为公差的等差数列.
∴2ak+1=ak+ak+2,
原方程可转化为(akx+ak+2)(x+1)=0,
∴k取任何正整数,方程akx2+2ak+1x+ak+2=0都有一个相同的实根-1;
(2)由题意,原方程另一根为xn,xn=-
| ak+2 |
| ak |
| 2d |
| ak |
∴1+xn=-
| 2d |
| ak |
∴
| 1 |
| 1+xn |
| ak |
| 2d |
∴
| 1 |
| 1+xn+1 |
| 1 |
| 1+xn |
| ak-ak+1 |
| 2d |
| 1 |
| 2 |
∴数列{
| 1 |
| 1+xn |
| 1 |
| 1+an |
| 1 |
| 2 |
点评:本题考查等差关系得确定,考查方程思想与推理运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
质点运动规律为s=t2-3,则在时间(3,3+△t)中相应的平均速度为( )
| A、3 | B、6 | C、9 | D、12 |
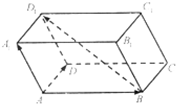 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为平行四边形,已知
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为平行四边形,已知| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| a |
| b |
| c |
| BD1 |
A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、-
|
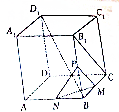 如图,在棱长为2的正方体ABCD一A1B1C1D1中,M为BC的中点,N为AB的中点,P为BB1的中点.
如图,在棱长为2的正方体ABCD一A1B1C1D1中,M为BC的中点,N为AB的中点,P为BB1的中点.