题目内容
若a=
cosxdx,则二项式(a
-
)4的展开式中的常数项为 .
| ∫ |
-
|
| x |
| 1 | ||
|
考点:定积分,二项式系数的性质
专题:二项式定理
分析:运用积分公式得出a=2,二项式(2
-
)4的展开式中项为:Tr+1=
•24-r•(-1)•x2-r,
利用常数项特征求解即可.
| x |
| 1 | ||
|
| C | r 4 |
利用常数项特征求解即可.
解答:
解:∵a=
cosxdx=sinx
=sin
-sin(-
)=2
∴a=2
∴二项式(2
-
)4的展开式中项为:Tr+1=
•24-r•(-1)•x2-r,
当2-r=0时,r=2,常数项为:
•4×1=6×4=24
故答案为:24
| ∫ |
-
|
| | |
-
|
| π |
| 2 |
| π |
| 2 |
∴a=2
∴二项式(2
| x |
| 1 | ||
|
| C | r 4 |
当2-r=0时,r=2,常数项为:
| C | 2 4 |
故答案为:24
点评:本题考察了积分与二项展开式定理,属于难度较小的综合题,关键是记住公式.

练习册系列答案
相关题目
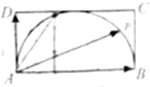 如图,矩形ABCD中,AB=2AD=2,点P在以AB为直径的半圆上移动,若
如图,矩形ABCD中,AB=2AD=2,点P在以AB为直径的半圆上移动,若| AP |
| AB |
| AD |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
从4名男生和3名女生中选出4人参加迎新座谈会,其中男生甲一定要入选,不同的选法共有 ( )
| A、120种 | B、24种 |
| C、20种 | D、12种 |