题目内容
已知:α,β是不同的平面,l,m,n是不同的直线,则下列说法正确的是( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
考点:空间中直线与平面之间的位置关系,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:利用面面垂直、面面平行、线面垂直的判定定理对四个选项分别分析选择正确答案.
解答:
解:对于A,因为过m的平面与β交于直线n,则m∥n,又l∥m,则l∥n,又l⊥α,所以n⊥α,n?β,所以α⊥β;故A正确;
对于B,l⊥m,m?α,直线l有可能在α内,所以B错误;
对于C,如果直线m,n平行,直线l可能在α内;故C 错误;
对于D,如果直线m,n平行,平面α,β可能相交;故D错误;
故选A.
对于B,l⊥m,m?α,直线l有可能在α内,所以B错误;
对于C,如果直线m,n平行,直线l可能在α内;故C 错误;
对于D,如果直线m,n平行,平面α,β可能相交;故D错误;
故选A.
点评:本题考查了面面垂直、面面平行、线面垂直的判定定理的运用;熟练掌握定理的条件是关键.

练习册系列答案
相关题目
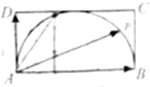 如图,矩形ABCD中,AB=2AD=2,点P在以AB为直径的半圆上移动,若
如图,矩形ABCD中,AB=2AD=2,点P在以AB为直径的半圆上移动,若| AP |
| AB |
| AD |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
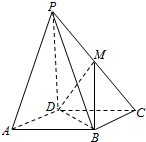 在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是边长为2的正方形,且PD=AB.
在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是边长为2的正方形,且PD=AB.