题目内容
已知函数f(x)=2lnx+
(m∈R)
(1)当m=2时,求函数f(x)在区间[
,e]上的最大值和最小值
(2)若x≥1,函数f(x)≤0恒成立,求m的取值范围.
| (m-1)(x2-1) |
| x |
(1)当m=2时,求函数f(x)在区间[
| 1 |
| 2 |
(2)若x≥1,函数f(x)≤0恒成立,求m的取值范围.
考点:利用导数求闭区间上函数的最值,函数的最值及其几何意义,函数恒成立问题
专题:综合题,导数的综合应用
分析:(1)求导数,确定函数f(x)在区间[
,e]上单调递增,即可求函数f(x)在区间[
,e]上的最大值和最小值
(2)若x≥1,函数f(x)≤0恒成立,等价于m-1≤
,求出
<0,即可求m的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
(2)若x≥1,函数f(x)≤0恒成立,等价于m-1≤
| 2xlnx |
| 1-x2 |
| 2xlnx |
| 1-x2 |
解答:
解:(1)当m=2时,f(x)=2lnx+x-
,
∴f′(x)=
+1+
,
∴函数f(x)在区间[
,e]上单调递增,
∴函数f(x)在区间[
,e]上的最大值为2+e-
,最小值为-2ln2-
;
(2)x≥1,2lnx+
≤0等价于m-1≤
,
设y=2xlnx,则y′=-2lnx-2,
∵x≥1,∴函数在(1,+∞)上单调递减,
从而g(x)=
在(1,+∞)上单调递减,
∴g(x)<0,
∴m-1≤0,
∴m≤1.
| 1 |
| x |
∴f′(x)=
| 2 |
| x |
| 1 |
| x2 |
∴函数f(x)在区间[
| 1 |
| 2 |
∴函数f(x)在区间[
| 1 |
| 2 |
| 1 |
| e |
| 3 |
| 2 |
(2)x≥1,2lnx+
| (m-1)(x2-1) |
| x |
| 2xlnx |
| 1-x2 |
设y=2xlnx,则y′=-2lnx-2,
∵x≥1,∴函数在(1,+∞)上单调递减,
从而g(x)=
| 2xlnx |
| 1-x2 |
∴g(x)<0,
∴m-1≤0,
∴m≤1.
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
从4名男生和3名女生中选出4人参加迎新座谈会,其中男生甲一定要入选,不同的选法共有 ( )
| A、120种 | B、24种 |
| C、20种 | D、12种 |
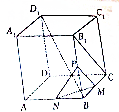 如图,在棱长为2的正方体ABCD一A1B1C1D1中,M为BC的中点,N为AB的中点,P为BB1的中点.
如图,在棱长为2的正方体ABCD一A1B1C1D1中,M为BC的中点,N为AB的中点,P为BB1的中点.