题目内容
7.函数f(x)=x2-2x+4的单调递增区间为[1,+∞).分析 求出二次函数的对称轴,判断开口方向,即可写出结果.
解答 解:函数f(x)=x2-2x+4的开口向上,对称轴为:x=1,
函数f(x)=x2-2x+4的单调递增区间为[1,+∞)(写成(1,+∞)也对).
故答案为:[1,+∞).
点评 本题考查二次函数的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
18.已知函数f(x)=cos(ωx+φ)(ω>0)图象的两条相邻对称轴之间距离是$\frac{π}{2}$,若f(x)≤f($-\frac{7π}{8}$),则函数y=sin(ωx+φ)一个单调递增区间是( )
| A. | $[-\frac{3π}{8},\frac{π}{8}]$ | B. | $[\frac{π}{8},\frac{5π}{8}]$ | C. | $[-\frac{5π}{8},-\frac{π}{8}]$ | D. | $[-\frac{π}{8},\frac{3π}{8}]$ |
12.已知函数f(x)=9x-m•3x+1,在(0,+∞)的图象恒在x轴上方,则m的取值范围是( )
| A. | m>2 | B. | m≥2 | C. | m≤2 | D. | m<2 |
16.设集合M={1,2},则满足条件M∪N={1,2,6}的集合N的个数是( )
| A. | 1 | B. | 3 | C. | 2 | D. | 4 |
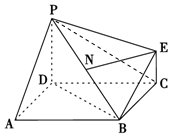 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2,N为线段PB的中点.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2,N为线段PB的中点.