题目内容
18.已知函数f(x)=cos(ωx+φ)(ω>0)图象的两条相邻对称轴之间距离是$\frac{π}{2}$,若f(x)≤f($-\frac{7π}{8}$),则函数y=sin(ωx+φ)一个单调递增区间是( )| A. | $[-\frac{3π}{8},\frac{π}{8}]$ | B. | $[\frac{π}{8},\frac{5π}{8}]$ | C. | $[-\frac{5π}{8},-\frac{π}{8}]$ | D. | $[-\frac{π}{8},\frac{3π}{8}]$ |
分析 利用三角函数的图象的对称性,三角函数的周期性求得ω,余弦函数的最值求得φ,再利用正弦函数的单调性求得函数y=sin(ωx+φ)一个单调递增区间.
解答 解:由题意可得$\frac{1}{2}•\frac{2π}{ω}$=$\frac{π}{2}$,∴ω=2.
再根据f(x)≤f($-\frac{7π}{8}$),可得2•(-$\frac{7π}{8}$)+φ=2kπ,k∈Z,
∴φ=-$\frac{π}{4}$,函数f(x)=cos(2x-$\frac{π}{4}$).
故函数y=sin(ωx+φ)=sin(2x-$\frac{π}{4}$),
令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{π}{8}$≤x≤kπ+$\frac{3π}{8}$,
可得函数的增区间为[kπ-$\frac{π}{8}$,kπ+$\frac{3π}{8}$],k∈Z,
故选:D.
点评 本题主要考查三角函数的图象的对称性,三角函数的周期性、单调性、最值,属于基础题.

练习册系列答案
相关题目
6.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{a}(x≥0)}\\{|x-2|(x<0)}\end{array}\right.$,且f(-2)=f(2),则f(4)=( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
8.下列各对象可以组成集合的是( )
| A. | 中国著名的科学家 | |
| B. | 2016感动中国十大人物 | |
| C. | 高速公路上接近限速速度行驶的车辆 | |
| D. | 中国最美的乡村 |
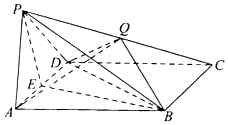 已知四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,E是AD的中点,点Q在侧棱PC上.
已知四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,E是AD的中点,点Q在侧棱PC上.