题目内容
2.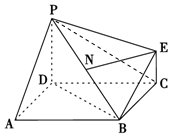 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2,N为线段PB的中点.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2,N为线段PB的中点.(Ⅰ)证明:NE⊥PD;
(Ⅱ)求三棱锥E-PBC的体积.
分析 (Ⅰ)连结AC与BD交于点F,则F为BD的中点,连结NF,由三角形中位线定理可得NF∥PD,$NF=\frac{1}{2}PD$,在结合已知得四边形NFCE为平行四边形,得到NE∥AC.再由PD⊥平面ABCD,得AC⊥PD,从而证得NE⊥PD;
(Ⅱ)由PD⊥平面ABCD,得平面PDCE⊥平面ABCD,可得BC⊥CD,则BC⊥平面PDCE.然后利用等积法把三棱锥E-PBC的体积转化为B-PEC的体积求解.
解答 (Ⅰ)证明:连结AC与BD交于点F,则F为BD的中点,连结NF,
∵N为线段PB的中点,∴NF∥PD,且$NF=\frac{1}{2}PD$,
又EC∥PD且$EC=\frac{1}{2}PD$,
∴NF∥EC且NF=EC.
∴四边形NFCE为平行四边形,
∴NE∥FC,即NE∥AC.
又∵PD⊥平面ABCD,AC?面ABCD,
∴AC⊥PD,
∵NE∥AC,∴NE⊥PD;
(Ⅱ)解:∵PD⊥平面ABCD,PD?平面PDCE,
∴平面PDCE⊥平面ABCD,
∵BC⊥CD,平面PDCE∩平面ABCD=CD,BC?平面ABCD,
∴BC⊥平面PDCE.
三棱锥E-PBC的体积${V_{E-PBC}}={V_{B-PEC}}=\frac{1}{3}{S_{△PEC}}•BC$=$\frac{1}{3}×\frac{1}{2}×1×2×2=\frac{2}{3}$.
点评 本题考查空间中直线与直线的位置关系,考查了线面垂直的性质,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
相关题目
12.已知函数f(x)=$\frac{2{x}^{2}-1}{{x}^{2}+2}$,则函数f(x)的值域是( )
| A. | [-$\frac{1}{2}$,1] | B. | [-$\frac{1}{2}$,2] | C. | [-$\frac{1}{2}$,2) | D. | (-$\frac{1}{2}$,1) |
17.已知定义在R上的函数y=f(x)满足:函数y=f(x-1)的图象关于直线x=1对称,且当x∈(-∞,0),f(x)+xf′(x)<0成立(f′(x)是函数f(x)的导函数),若a=(sin$\frac{1}{2}$)f(sin$\frac{1}{2}$),b=(ln2)f(ln2),c=2f(log${\;}_{\frac{1}{2}}$$\frac{1}{4}$),则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
14.试用集合A,B的交集、并集、补集表示图中阴影部分所表示的集合( )


| A. | ∁UB | B. | A∩(∁UB) | C. | A∪(∁UB) | D. | ∁U(A∩B) |
