题目内容
19.已知函数f(x)=$\frac{{x}^{2}}{1+{x}^{2}}$(1)求f(2)与f($\frac{1}{2}$),f(3)与f($\frac{1}{3}$)(2)证明:f(x)+f($\frac{1}{x}$)=1.
分析 (1)由f(x)=$\frac{{x}^{2}}{1+{x}^{2}}$=1-$\frac{1}{{x}^{2}+1}$,能求出求f(2)与f($\frac{1}{2}$),f(3)与f($\frac{1}{3}$)的值.
(2)由f(x)=$\frac{{x}^{2}}{1+{x}^{2}}$,能证明f(x)+f($\frac{1}{x}$)=1.
解答 解:(1)由f(x)=$\frac{{x}^{2}}{1+{x}^{2}}$=1-$\frac{1}{{x}^{2}+1}$,
∴f(2)=1-$\frac{1}{{2}^{2}+1}$=$\frac{4}{5}$,f($\frac{1}{2}$)=1-$\frac{1}{\frac{1}{4}+1}$=$\frac{1}{5}$.
f(3)=1-$\frac{1}{{3}^{2}+1}$=$\frac{9}{10}$,f($\frac{1}{3}$)=1-$\frac{1}{\frac{1}{9}+1}$=$\frac{1}{10}$.
证明:(2)∵f(x)=$\frac{{x}^{2}}{1+{x}^{2}}$,
∴f(x)+f($\frac{1}{x}$)=$\frac{{x}^{2}}{1+{x}^{2}}$+$\frac{\frac{1}{{x}^{2}}}{1+\frac{1}{{x}^{2}}}$
=$\frac{{x}^{2}}{1+{x}^{2}}$+$\frac{1}{{x}^{2}+1}$=1.
故f(x)+f($\frac{1}{x}$)=1.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
14.试用集合A,B的交集、并集、补集表示图中阴影部分所表示的集合( )


| A. | ∁UB | B. | A∩(∁UB) | C. | A∪(∁UB) | D. | ∁U(A∩B) |
4.数列{an}满足an=4an-1+3,a2=3,则此数列的第5项是( )
| A. | 15 | B. | 255 | C. | 20 | D. | 8 |
8.下列各对象可以组成集合的是( )
| A. | 中国著名的科学家 | |
| B. | 2016感动中国十大人物 | |
| C. | 高速公路上接近限速速度行驶的车辆 | |
| D. | 中国最美的乡村 |
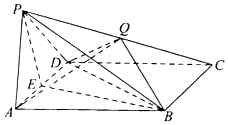 已知四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,E是AD的中点,点Q在侧棱PC上.
已知四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,E是AD的中点,点Q在侧棱PC上.