题目内容
17.已知函数f(x)为定义域在(0,+∞)上的增函数,且满足f(2)=1,f(xy)=f(x)+(y)(1)求f(1),f(4)的值.
(2)如果f(8-x)-f(x-3)≤4,求x的取值范围.
分析 (1)令x=y=1,可求出f(1),令x=y=2,结合条件,可求出f(4);
(2)将4换成f(16),结合条件得到f(8-x)<f(16(x-3)),再由单调性,即可求出x的取值范围,注意定义域.
解答 解:(1)∵f(xy)=f(x)+f(y),∴令x=y=1,则f(1)=2f(1),即f(1)=0,
令x=y=2,则f(4)=2f(2)=2.
(2)令x=y=4,则f(16)=2f(4)=4.
不等式f(8-x)-f(x-3)≤4,即f(8-x)≤f(x-3)+4
即f(8-x)≤f(x-3)+f(16)=f(16(x-3)
由于函数在定义域(0,+∞)上为增函数,⇒
$\left\{\begin{array}{l}{8-x>0}\\{x-3>0}\\{8-x≤16(x-3)}\end{array}\right.$ 解得不等式组得:$\frac{56}{17}≤x<8$
所以x的取值范围:[$\frac{56}{17}$,8)
点评 本题主要考查函数的单调性及运用,考查解决抽象函数值的常用方法:赋值法,属于基础题

练习册系列答案
相关题目
7.已知a=0.21.5,b=20.1,c=0.21.3,则a,b,c的大小关系是( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | b<c<a |
12.已知函数f(x)=$\frac{2{x}^{2}-1}{{x}^{2}+2}$,则函数f(x)的值域是( )
| A. | [-$\frac{1}{2}$,1] | B. | [-$\frac{1}{2}$,2] | C. | [-$\frac{1}{2}$,2) | D. | (-$\frac{1}{2}$,1) |
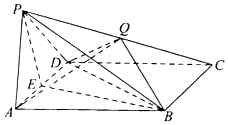 已知四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,E是AD的中点,点Q在侧棱PC上.
已知四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,E是AD的中点,点Q在侧棱PC上.