题目内容
若（ax2+
）5的展开式中的常数项为80，则（y+2）2a展开式中所有系数的和等于 ．
| 1 |
| x3 |
考点：二项式系数的性质
专题：二项式定理
分析：通过二项式的展开式中的常数项为80求出a，通过y=1求出（y+2）2a展开式中所有系数的和即可．
解答：
解：解：（ax2+
）5的展开式中的常数项为80，所以
•a3=80，解得a=2．
（y+2）2a化为：（y+2）4展开式中所有系数的和即为y=1时，即（1+2）4=81．
故答案为：81．
| 1 |
| x3 |
| C | 2 5 |
（y+2）2a化为：（y+2）4展开式中所有系数的和即为y=1时，即（1+2）4=81．
故答案为：81．
点评：本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数．
练习册系列答案
相关题目
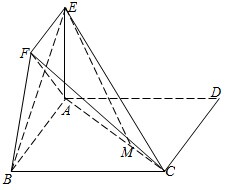如图，四边形ABCD为正方形，EA⊥平面ABCD，EF∥AB，AB=4，AE=2，EF=1，
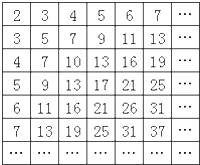表中的数阵为“森德拉姆数筛”，其特点是每行每列都成等差数列，记第i行第j列的数为aij．则数列{an}满足an+2-2an+1+an=0（n∈N*），a1=31，a2=29，则该数列中相邻两项的乘积是负数的是（ ）
| A、a14a15 |
| B、a15a16 |
| C、a16a17 |
| D、a17a18 |