Question

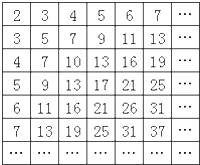表中的数阵为“森德拉姆数筛”，其特点是每行每列都成等差数列，记第i行第j列的数为a_ij．则
（1）a_nn=

 

（n∈N^*）；
（2）表中的数52共出现

 

次．

Answer 1

考点：等差数列的通项公式

专题：等差数列与等比数列

分析：a_nn表示第n行第n列的数，由题意知第n行是首项为n+1，公差为n的等差数列，由此能求出a_nn；利用观察法及定义可知第1行数组成的数列A_1j（j=1，2，）是以2为首项，公差为1的等差数列，进一步分析得知第j列数组成的数列A_1j（i=1，2，）是以j+1为首项，公差为j的等差数列，同时分别求出通项公式，从而得知结果．

解答： 解：a_nn表示第n行第n列的数，
由题意知第n行是首项为n+1，公差为n的等差数列，
∴a_nn=（n+1）+（n-1）×n=n²+1．
第i行第j列的数记为A_ij．那么每一组i与j的解就是表中一个数．
因为第一行数组成的数列A_1j（j=1，2，）是以2为首项，公差为1的等差数列，
所以A_1j=2+（j-1）×1=j+1，
所以第j列数组成的数列A_1j（i=1，2，）是以j+1为首项，公差为j的等差数列，
所以A_ij=j+1+（i-1）×j=ij+1．
令A_ij=ij+1=52，
即ij=51=1×51=17×3=3×17=51×1，
故表中52共出现4次．
故答案为：n²+1，4．

点评：此题考查行列模型的等差数列的求法，是基础题，解题时要熟练掌握等差数列的性质．