题目内容
数列{an}的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,其中n∈N*.
(1)若数列{an}是等比数列,求实数t的值;
(2)设各项均不为0的数列{cn}中,所有满足ci•ci+1<0的整数i的个数称为这个数列{cn}的“积异号数”,令cn=
(n∈N*),在(1)的条件下,求数列{cn}的“积异号数”
(1)若数列{an}是等比数列,求实数t的值;
(2)设各项均不为0的数列{cn}中,所有满足ci•ci+1<0的整数i的个数称为这个数列{cn}的“积异号数”,令cn=
| nan-4 |
| nan |
考点:数列与函数的综合,等比关系的确定
专题:等差数列与等比数列
分析:(1)由题意,当n≥2时,有
,两式相减,得an+1-an=2an,由此能求出t=1.
(2)由(1)得an=3n-1,从而cn=
=
=1-
,由此能求出数列{cn}的“积异号数”为1.
|
(2)由(1)得an=3n-1,从而cn=
| nan-4 |
| nan |
| n•3n-1-1 |
| n•3n-1 |
| 4 |
| n•3n-1 |
解答:
解:(1)由题意,当n≥2时,有
,
两式相减,得an+1-an=2an,
∴an+1=3an,n≥2,
∴当n≥2时,{an}是等比数列,
要使n≥1时,{an}是等比数列,
则只需
=
=3,
解得t=1.
(2)由(1)得等比数列{an}的首项为a1=1,公比为q=3,
∴an=3n-1,
∴cn=
=
=1-
,
∵c1=1-
=-3,c2=1-
=
,
∴c1c2=-1<0,
∵cn+1-cn=
-
=
>0,
∴{cn}递增,由c2=
>0,得n≥2时,cn>0,
∴数列{cn}的“积异号数”为1.
|
两式相减,得an+1-an=2an,
∴an+1=3an,n≥2,
∴当n≥2时,{an}是等比数列,
要使n≥1时,{an}是等比数列,
则只需
| a2 |
| a1 |
| 2t+1 |
| t |
解得t=1.
(2)由(1)得等比数列{an}的首项为a1=1,公比为q=3,
∴an=3n-1,
∴cn=
| nan-4 |
| nan |
| n•3n-1-1 |
| n•3n-1 |
| 4 |
| n•3n-1 |
∵c1=1-
| 4 |
| 1 |
| 4 |
| 2×3 |
| 1 |
| 3 |
∴c1c2=-1<0,
∵cn+1-cn=
| 4 |
| n•3n-1 |
| 4 |
| (n+1)•3n |
| 4(2n+3) |
| n(n+1)•3n |
∴{cn}递增,由c2=
| 1 |
| 3 |
∴数列{cn}的“积异号数”为1.
点评:本题考查实数t的值,数列{cn}的“积异号数”的求法,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
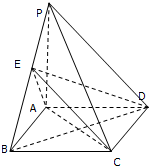 四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=
四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=