题目内容
已知椭圆C:
+
=1与双曲线
+
=1(1<v<4)有公共焦点,过椭圆C的右顶点B任意作直线l,设直线l交抛物线y2=2x于P、Q两点,且OP⊥OQ.
(Ⅰ)求椭圆C的方程;
(Ⅱ)在椭圆C上,是否存在点R(m,n)使得直线l:mx+ny=1与圆O:x2+y2=1相交于不同的两点M、N,且△OMN的面积最大?若存在,求出点R的坐标及对应的△OMN的面积;若不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 4-v |
| y2 |
| 1-v |
(Ⅰ)求椭圆C的方程;
(Ⅱ)在椭圆C上,是否存在点R(m,n)使得直线l:mx+ny=1与圆O:x2+y2=1相交于不同的两点M、N,且△OMN的面积最大?若存在,求出点R的坐标及对应的△OMN的面积;若不存在,请说明理由.
考点:圆锥曲线的综合
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)先确定c,利用椭圆C与双曲线共焦点,知a2-b2=3,设直线l的方程为x=ty+a,代入y2=2x,利用OP⊥OQ,即可求出a,b,即可求椭圆C的方程;
(Ⅱ)由题意可知:当且仅当∠AOB=90°时,△AOB的面积取得最大值,得出m,n满足的关系式,与m2+4n2=4联立解出即可.
(Ⅱ)由题意可知:当且仅当∠AOB=90°时,△AOB的面积取得最大值,得出m,n满足的关系式,与m2+4n2=4联立解出即可.
解答:
解:(Ⅰ)∵1<v<4,
∴双曲线的焦点在x轴上,设F(±c,0),
则c2=4-v+v-1=3,
由椭圆C与双曲线共焦点,知a2-b2=3,
设直线l的方程为x=ty+a,代入y2=2x,可得y2-2ty-2a=0,
设P(x1,y1),Q(x2,y2),则y1+y2=2t,y1y2=-2a,
∵OP⊥OQ,
∴x1x2+y1y2=a2-2a=0,
∴a=2,b=1,
∴椭圆C的方程为
+y2=1;
(Ⅱ)在△MON中,S△OMN=
|OM||ON|sin∠MON=
sin∠MON
当∠MON=90°时,sin∠MON有最大值
,
此时点O到直线L的距离为d=
=
.
∴m2+n2=2.
又∵m2+4n2=4,
联立
,
解得m2=
,n2=
,此时点R(
,±
)或(-
,±
),△MON的面积为
.
∴双曲线的焦点在x轴上,设F(±c,0),
则c2=4-v+v-1=3,
由椭圆C与双曲线共焦点,知a2-b2=3,
设直线l的方程为x=ty+a,代入y2=2x,可得y2-2ty-2a=0,
设P(x1,y1),Q(x2,y2),则y1+y2=2t,y1y2=-2a,
∵OP⊥OQ,
∴x1x2+y1y2=a2-2a=0,
∴a=2,b=1,
∴椭圆C的方程为
| x2 |
| 4 |
(Ⅱ)在△MON中,S△OMN=
| 1 |
| 2 |
| 1 |
| 2 |
当∠MON=90°时,sin∠MON有最大值
| 1 |
| 2 |
此时点O到直线L的距离为d=
| 1 | ||
|
| ||
| 2 |
∴m2+n2=2.
又∵m2+4n2=4,
联立
|
解得m2=
| 4 |
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
| 1 |
| 2 |
点评:本题考查椭圆的标准方程,考查三角形面积的求解,考查学生分析解决问题的能力,正确表示三角形的面积是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设函数f(x)=(x-1)kcosx(k∈N*),则( )
| A、当k=2013时,f(x)在x=1处取得极小值 |
| B、当k=2013时,f(x)在x=1处取得极大值 |
| C、当k=2014时,f(x)在x=1处取得极小值 |
| D、当k=2014时,f(x)在x=1处取得极大值 |
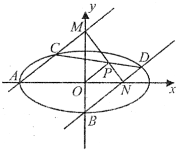 如图,过椭圆L的左顶点A(-3,0)和下顶点B且斜率均为k的两直线l1,l2分别交椭圆于C,D,又l1交y轴于M,l2交x轴于N,且CD与MN相交于点P,当k=3时,△ABM是直角三角形.
如图,过椭圆L的左顶点A(-3,0)和下顶点B且斜率均为k的两直线l1,l2分别交椭圆于C,D,又l1交y轴于M,l2交x轴于N,且CD与MN相交于点P,当k=3时,△ABM是直角三角形.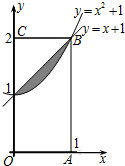 如图,在矩形OABC内:记抛物线y=x2+1与直线y=x+1围成的区域为M(图中阴影部分).随机往矩形OABC内投一点P,则点P落在区域M内的概率是( )
如图,在矩形OABC内:记抛物线y=x2+1与直线y=x+1围成的区域为M(图中阴影部分).随机往矩形OABC内投一点P,则点P落在区域M内的概率是( )