题目内容
己知命题p:椭圆
+
=1,长轴在y轴上.
(Ⅰ)若椭圆焦距为4,求实数m的值;
(Ⅱ)命题q:关于x的不等式x2-2x+m>0的解集是R;若“p∧q”是假命题,“p∨q”是真命题,求实数m的取值范围.
| x2 |
| 10-m |
| y2 |
| m-2 |
(Ⅰ)若椭圆焦距为4,求实数m的值;
(Ⅱ)命题q:关于x的不等式x2-2x+m>0的解集是R;若“p∧q”是假命题,“p∨q”是真命题,求实数m的取值范围.
考点:命题的真假判断与应用,直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程,简易逻辑
分析:(Ⅰ)利用椭圆焦距为4,长轴在y轴上,直接求实数m的值;
(Ⅱ)先求命题p和命题q为真时m取值范围,再根据复合命题真值表判断命题p、q一真一假,分p真q假时和p假q真时两种情况求解.
(Ⅱ)先求命题p和命题q为真时m取值范围,再根据复合命题真值表判断命题p、q一真一假,分p真q假时和p假q真时两种情况求解.
解答:
解:(Ⅰ)椭圆焦距为4,长轴在y轴上,∴4=(m-2)-(10-m),解得m=8.
(Ⅱ)命题p为真时,m-2>10-m>0⇒10>m>6;
命题q为真时,△=4-4m<0⇒m>1;
若“p∧q”是假命题,“p∨q”是真命题,由复合命题真值表得,p、q一真一假,
若p真q假时,则
⇒m∈∅;
若p假q真时,则
⇒1<m≤6或m≥10;
综上实数m的取值范围是1<m≤6或m≥10.即m∈(1,6]∪[10,+∞).
(Ⅱ)命题p为真时,m-2>10-m>0⇒10>m>6;
命题q为真时,△=4-4m<0⇒m>1;
若“p∧q”是假命题,“p∨q”是真命题,由复合命题真值表得,p、q一真一假,
若p真q假时,则
|
若p假q真时,则
|
综上实数m的取值范围是1<m≤6或m≥10.即m∈(1,6]∪[10,+∞).
点评:本题借助考查复合命题的真假判定,考查了椭圆的标准方程,不等式的恒成立问题,要求熟记复合命题真值表.

练习册系列答案
相关题目
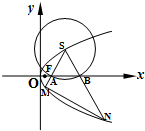 如图,已知点F是抛物线C:y2=x的焦点,S是抛物线C在第一象限内的点,且|SF|=
如图,已知点F是抛物线C:y2=x的焦点,S是抛物线C在第一象限内的点,且|SF|= 如图,已知直线l:y=2x-4交抛物线y2=4x于A、B两点,试在抛物线AOB这段曲线上求一点P,使△ABP的面积最大,并求这个最大面积.
如图,已知直线l:y=2x-4交抛物线y2=4x于A、B两点,试在抛物线AOB这段曲线上求一点P,使△ABP的面积最大,并求这个最大面积.