Question

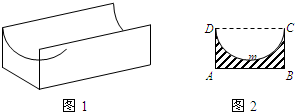图1是某种称为“凹槽”的机械部件的示意图，图2是凹槽的横截面（阴影部分）示意图，示意图，其中四边形ABCD是矩形，弧CmD是半圆，凹槽的横截面的周长为4．设AB=2x，BC=y，凹槽的强度与横截面的面积的x倍成正比，且当AB=1时凹槽的强度为

4-π

16

．
（1）写出y关于x的函数表达式，并指出x的取值范围；
（2）求当x取何值时，凹槽的强度最大，并求出最大值．

Answer 1

考点：导数在最大值、最小值问题中的应用

专题：应用题,导数的综合应用

分析：（1）由“其中四边形ABCD是矩形，弧CmD是半圆，凹槽的横截面的周长为4”建立模型，再根据四边形ABCD是矩形求得定义域．
（2）先求得横断面的面积，再由凹槽的强度与横截面的面积的x倍成正比，且当AB=1时凹槽的强度为

4-π

16

，建立模型，用导数法求得最值．

解答： 解：（1）易知半圆CmD的半径为x，故半圆CmD的弧长为πx．
所以4=2x+2y+πx，
得y=

4-(2+π)x

2

依题意知：0＜x＜y
得0＜x＜

4

4+π

所以，y=

4-(2+π)x

2

（0＜x＜

4

4+π

）．
（2）依题意，设凹槽的强度为T，横截面的面积为S，凹槽的强度与横截面的面积的x倍成正比的比例系数为k，
则有T=kxS=

3

x（2xy-

πx2

2

）=k[4x²-（2+

3π

2

）x³]
由已知当x=

1

2

时，y=

4-π

16

，解得k=

1

3

所以T=

1

3

[4x²-（2+

3π

2

）x³]（0＜x＜

4

4+π

）．
所以T′=（2+

3π

2

）x[

4

3(2+ 3π 2 )

-x]
令T′=0得x=

16

3(4+3π)

，
x∈（0，

16

3(4+3π)

）时，T′＞0；x∈（

16

3(4+3π)

，

4

4+π

）时，T′＜0
所以，当x=

16

3(4+3π)

时，T的最大值为

1024

81(4+3π)2

．

点评：本题主要考查数学建模型和解模型的能力，主要涉及了平面图形的周长，面积及在实际问题中模型的意义．