题目内容
(1)在△ABC中,已知a=1,b=1,C=120°,求c;
(2)在△ABC中,A=
,a=8,b=8
,求△ABC面积S.
(2)在△ABC中,A=
| π |
| 6 |
| 3 |
考点:正弦定理,余弦定理
专题:解三角形
分析:(1)由已知得A=B=30°,
=
,由此能求出c.
(2)由正弦定理得
=
,从而sinB=
,由△ABC面积S=
absinB,能求出结果.
| 1 |
| sin30° |
| c |
| sin120° |
(2)由正弦定理得
| 8 | ||
sin
|
8
| ||
| sinB |
| 3 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)∵在△ABC中,a=1,b=1,C=120°,
∴A=B=
=30°,
∴
=
,
∴c=
=
×2=
.
(2)∵在△ABC中,A=
,a=8,b=8
,
∴
=
,解得sinB=
=
,
∴△ABC面积S=
absinB=
×8×8
×
=48
.
∴A=B=
| 180°-120° |
| 2 |
∴
| 1 |
| sin30° |
| c |
| sin120° |
∴c=
| 1×sin60° |
| sin30° |
| ||
| 2 |
| 3 |
(2)∵在△ABC中,A=
| π |
| 6 |
| 3 |
∴
| 8 | ||
sin
|
8
| ||
| sinB |
8
| ||
| 8 |
| 3 |
| 2 |
∴△ABC面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
点评:本题考查三角形的边长的求法,考查三角形的面积的求法,解题时要认真审题,注意正弦定理的合理运用.

练习册系列答案
相关题目
若2弧度的圆心角所对的弧长为2cm,则这个圆心角所夹的扇形的面积是( )
| A、4 cm2 |
| B、2 cm2 |
| C、4π cm2 |
| D、1 cm2 |
cos2
-sin2
=( )
| π |
| 12 |
| π |
| 12 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
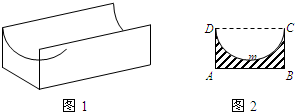 图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,示意图,其中四边形ABCD是矩形,弧CmD是半圆,凹槽的横截面的周长为4.设AB=2x,BC=y,凹槽的强度与横截面的面积的x倍成正比,且当AB=1时凹槽的强度为
图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,示意图,其中四边形ABCD是矩形,弧CmD是半圆,凹槽的横截面的周长为4.设AB=2x,BC=y,凹槽的强度与横截面的面积的x倍成正比,且当AB=1时凹槽的强度为 如图,已知AB是平面α的一条斜线,B为斜足,AO⊥α,O为垂足,BC为α内的一条直线,∠ABC=60°,∠OBC=45°,求斜线AB和平面α所成角.
如图,已知AB是平面α的一条斜线,B为斜足,AO⊥α,O为垂足,BC为α内的一条直线,∠ABC=60°,∠OBC=45°,求斜线AB和平面α所成角.