题目内容
已知函数f(x)=klnx-kx-3(k∈R).
(Ⅰ)当k=-1时,求函数f(x)的单调区间;
(Ⅱ)若函数y=f(x)的图象在(2,f(2))处的切线与直线x-y-3=0平行,且函数g(x)=x3+
x2+x2f'(x) 在区间(1,2)上有极值,求t的取值范围.
(Ⅰ)当k=-1时,求函数f(x)的单调区间;
(Ⅱ)若函数y=f(x)的图象在(2,f(2))处的切线与直线x-y-3=0平行,且函数g(x)=x3+
| t |
| 2 |
考点:利用导数研究函数的单调性,利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(I)分别解出f′(x)>0,f′(x)<0 即可得出.
(II)由函数y=f(x)的图象在(2,f(2))处的切线与直线x-y-3=0平行,可得f′(2)=1,解出k=-2,f′(x)=
+2.可得g′(x)=3x2+(t+4)x-2,由于函数g(x)在区间(1,2)上存在极值,注意到y=g′(x)的图象为开口向上的抛物线,且g′(0)=-2<0,因此只需
,解出即可.
(II)由函数y=f(x)的图象在(2,f(2))处的切线与直线x-y-3=0平行,可得f′(2)=1,解出k=-2,f′(x)=
| -2 |
| x |
|
解答:
解:f′(x)=
-k(x>0).
(Ⅰ)当k=-1 时,f′(x)=-
+1=
,
令f′(x)>0 时,解得x>1,令f′(x)<0 时,解得0<x<1,
∴f(x)的单调递增区间是(1,+∞),单调递减区间是(0,1).
(Ⅱ)∵函数y=f(x)的图象在(2,f(2))处的切线与直线x-y-3=0平行,
∴f′(2)=1,即
-k=1,
∴k=-2,f′(x)=
+2,
g(x)=x3+(
+2)x2-2x,
∴g′(x)=3x2+(t+4)x-2,
∵函数g(x)在区间(1,2)上存在极值,
注意到y=g′(x)的图象为开口向上的抛物线,且g′(0)=-2<0,
∴只需
,
解得-9<t<-5,
∴t 的取值范围为(-9,-5).
| k |
| x |
(Ⅰ)当k=-1 时,f′(x)=-
| 1 |
| x |
| x-1 |
| x |
令f′(x)>0 时,解得x>1,令f′(x)<0 时,解得0<x<1,
∴f(x)的单调递增区间是(1,+∞),单调递减区间是(0,1).
(Ⅱ)∵函数y=f(x)的图象在(2,f(2))处的切线与直线x-y-3=0平行,
∴f′(2)=1,即
| k |
| 2 |
∴k=-2,f′(x)=
| -2 |
| x |
g(x)=x3+(
| t |
| 2 |
∴g′(x)=3x2+(t+4)x-2,
∵函数g(x)在区间(1,2)上存在极值,
注意到y=g′(x)的图象为开口向上的抛物线,且g′(0)=-2<0,
∴只需
|
解得-9<t<-5,
∴t 的取值范围为(-9,-5).
点评:本题考查了利用导数研究函数的单调性极值与最值、导数的几何意义、二次函数的单调性,考查了数形结合的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
函数f(x)是定义在区间[-5,5]上的偶函数,且在[0,5]上是单调函数,f(1)<f(3),则下列各式一定成立的是( )
| A、f(0)>f(5) |
| B、f(3)<f(2) |
| C、f(-1)>f(3) |
| D、f(-2)>f(1) |
cos2
-sin2
=( )
| π |
| 12 |
| π |
| 12 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
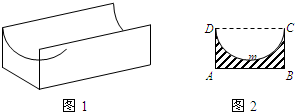 图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,示意图,其中四边形ABCD是矩形,弧CmD是半圆,凹槽的横截面的周长为4.设AB=2x,BC=y,凹槽的强度与横截面的面积的x倍成正比,且当AB=1时凹槽的强度为
图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,示意图,其中四边形ABCD是矩形,弧CmD是半圆,凹槽的横截面的周长为4.设AB=2x,BC=y,凹槽的强度与横截面的面积的x倍成正比,且当AB=1时凹槽的强度为