题目内容
已知{an}是等比数列，a2=2，a3=
，则公比q=（ ）
| 1 |
| 4 |
A、-
| ||
| B、-2 | ||
| C、2 | ||
D、
|
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：根据等比数列的性质和题意求出公比q即可．
解答：
解：由题意得，公比q=
=
=
，
故选：D．
| a3 |
| a2 |
| ||
| 2 |
| 1 |
| 8 |
故选：D．
点评：本题主要考查了等比数列的性质的应用，属于基础题．
练习册系列答案
相关题目
已知数列{an}中，a1=1，当n≥2时，an=2an-1+1，则an=（ ）
| A、n2-1 |
| B、n2-2n+2 |
| C、2n-1 |
| D、2n-1+1 |
函数f（x）是定义域为R的偶函数，当x＞0时f（x）=-x+1，则当x＜0时，f（x）的表达式为（ ）
| A、f（x）=-x+1 |
| B、f（x）=-x-1 |
| C、f（x）=x+1 |
| D、f（x）=x-1 |
函数f（x）是定义在区间[-5，5]上的偶函数，且在[0，5]上是单调函数，f（1）＜f（3），则下列各式一定成立的是（ ）
| A、f（0）＞f（5） |
| B、f（3）＜f（2） |
| C、f（-1）＞f（3） |
| D、f（-2）＞f（1） |
过双曲线
-
=1（a＞0，b＞0）的左焦点F（-c，0）作圆（x-c）2+y2=c2的切线，切点为E，且该切线与双曲线的右支交于点A．若
=
（
+
），则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| OE |
| 1 |
| 2 |
| OF |
| OA |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
若2弧度的圆心角所对的弧长为2cm，则这个圆心角所夹的扇形的面积是（ ）
| A、4 cm2 |
| B、2 cm2 |
| C、4π cm2 |
| D、1 cm2 |
设集合A={x∈R|x+y=2}，集合B={x∈R|x≤2}，则A∩B=（ ）
| A、{2} | B、φ | C、A | D、B |
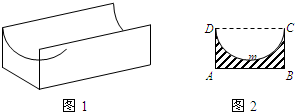图1是某种称为“凹槽”的机械部件的示意图，图2是凹槽的横截面（阴影部分）示意图，示意图，其中四边形ABCD是矩形，弧CmD是半圆，凹槽的横截面的周长为4．设AB=2x，BC=y，凹槽的强度与横截面的面积的x倍成正比，且当AB=1时凹槽的强度为