题目内容
已知数列{an}的各项均为正数,Sn是{an}的前n项和,对于任意的n∈N*,有2Sn=3an-3
(1)求数列{an}的通项公式;
(2)设{bn}的通项公式bn=
,{bn}的前n项和为Tn,若?n∈N*,a2-5a-
≤Tn恒成立,求a的取值范围.
(1)求数列{an}的通项公式;
(2)设{bn}的通项公式bn=
| 1 |
| log3an•log3an+2 |
| 17 |
| 3 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)当n=1时,2a1=2S1=3a1-3,解得a1=3.当n≥2时,2an=2(Sn-Sn-1),再利用等比数列的通项公式即可得出.
(2)bn=
=
=
(
-
),利用“裂项求和”可得Tn=
(1+
-
-
).利用其单调性可得Tn的最小值为T1=
.?n∈N*,a2-5a-
≤Tn恒成立??n∈N*,a2-5a--
≤(Tn)min=T1,再利用一元二次不等式的解法即可得出.
(2)bn=
| 1 |
| log3an•log3an+2 |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3 |
| 17 |
| 3 |
| 17 |
| 3 |
解答:
解:(1)当n=1时,2a1=2S1=3a1-3,解得a1=3.
当n≥2时,2an=2(Sn-Sn-1)=3an-3-(3an-1-3),化为an=3an-1.
∴数列{an}是等比数列,
∴an=a1qn-1=3n.
(2)bn=
=
=
(
-
),
∴{bn}的前n项和为Tn=
[(1-
)+(
-
)+(
-
)+…+(
-
)+(
-
)]
=
(1+
-
-
).
由上式可知:Tn对于n∈N*单调递增,∴当n=1时,Tn取得最小值,T1=
.
∵?n∈N*,a2-5a-
≤Tn恒成立??n∈N*,a2-5a--
≤(Tn)min=T1=
,
∴a2-5a-6≤0,
解得-1≤a≤6.
∴a的取值范围是[-1,6].
当n≥2时,2an=2(Sn-Sn-1)=3an-3-(3an-1-3),化为an=3an-1.
∴数列{an}是等比数列,
∴an=a1qn-1=3n.
(2)bn=
| 1 |
| log3an•log3an+2 |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
∴{bn}的前n项和为Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
由上式可知:Tn对于n∈N*单调递增,∴当n=1时,Tn取得最小值,T1=
| 1 |
| 3 |
∵?n∈N*,a2-5a-
| 17 |
| 3 |
| 17 |
| 3 |
| 1 |
| 3 |
∴a2-5a-6≤0,
解得-1≤a≤6.
∴a的取值范围是[-1,6].
点评:本题考查了等比数列的通项公式、递推式、“裂项求和”方法、恒成立问题的等价转化方法、一元二次不等式的解法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
设集合A={x∈R|x+y=2},集合B={x∈R|x≤2},则A∩B=( )
| A、{2} | B、φ | C、A | D、B |
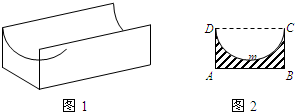 图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,示意图,其中四边形ABCD是矩形,弧CmD是半圆,凹槽的横截面的周长为4.设AB=2x,BC=y,凹槽的强度与横截面的面积的x倍成正比,且当AB=1时凹槽的强度为
图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,示意图,其中四边形ABCD是矩形,弧CmD是半圆,凹槽的横截面的周长为4.设AB=2x,BC=y,凹槽的强度与横截面的面积的x倍成正比,且当AB=1时凹槽的强度为 如图,已知AB是平面α的一条斜线,B为斜足,AO⊥α,O为垂足,BC为α内的一条直线,∠ABC=60°,∠OBC=45°,求斜线AB和平面α所成角.
如图,已知AB是平面α的一条斜线,B为斜足,AO⊥α,O为垂足,BC为α内的一条直线,∠ABC=60°,∠OBC=45°,求斜线AB和平面α所成角.