题目内容
设关于x的方程x2-mx-1=0有两个实根α,β(α<β),函数f(x)=
.
(Ⅰ)求证:不论m取何值,总有αf(α)=1;
(Ⅱ)判断f(x)在区间(α,β)的单调性,并加以证明;
(Ⅲ)若λ,μ均为正实数,证明:|f(
)-f(
)|<|α-β|.
| 2x-m |
| x2+1 |
(Ⅰ)求证:不论m取何值,总有αf(α)=1;
(Ⅱ)判断f(x)在区间(α,β)的单调性,并加以证明;
(Ⅲ)若λ,μ均为正实数,证明:|f(
| λα+μβ |
| λ+μ |
| μα+λβ |
| λ+μ |
考点:不等式的证明,利用导数研究函数的单调性
专题:综合题,不等式的解法及应用
分析:(Ⅰ)由α,β是方程x2-mx-1=0的两个实根,根据韦达定理,结合f(x)=
,化简,即可得出αf(α)=1;
(Ⅱ)利用f'(x)>0,可得结论;
(Ⅲ)证明|f(
)-f(
)|<|f(α)-f(β)|,由(Ⅰ)可知,f(α)=
,f(β)=
,αβ=-1,即可证明结论.
| 2x-m |
| x2+1 |
(Ⅱ)利用f'(x)>0,可得结论;
(Ⅲ)证明|f(
| λα+μβ |
| λ+μ |
| μα+λβ |
| λ+μ |
| 1 |
| α |
| 1 |
| β |
解答:
证明:(Ⅰ)∵α,β是方程x2-mx-1=0的两个根,∴α+β=m,αβ=-1,
∴f(α)=
=
=
=
,
∴αf(α)=1…(4分)
(Ⅱ)∵f′(x)=-
=-
,
当x∈(α,β)时,f'(x)>0,∴f(x)在(α,β)上单调递增;…(8分)
(Ⅲ)∵
-α=
>0,同理可证:α<
<β
∴由(Ⅱ)可知:f(α)<f(
)<f(β),f(α)<f(
)<f(β),
∴|f(
)-f(
)|<|f(α)-f(β)|,…(12分)
由(Ⅰ)可知,f(α)=
,f(β)=
,αβ=-1,
∴|f(α)-f(β)|=|
-
|=|
|=|α-β|,
∴|f(
)-f(
)|<|α-β|.…(14分)
∴f(α)=
| 2α-m |
| α2+1 |
| 2α-(α+β) |
| α2-αβ |
| α-β |
| α(α-β) |
| 1 |
| α |
∴αf(α)=1…(4分)
(Ⅱ)∵f′(x)=-
| 2(x2-mx-1) |
| (x2+1)2 |
| 2(x-α)(x-β) |
| (x2+1)2 |
当x∈(α,β)时,f'(x)>0,∴f(x)在(α,β)上单调递增;…(8分)
(Ⅲ)∵
| λα+μβ |
| λ+μ |
| μ(β-α) |
| λ+μ |
| λα+μβ |
| λ+μ |
∴由(Ⅱ)可知:f(α)<f(
| λα+μβ |
| λ+μ |
| μα+λβ |
| λ+μ |
∴|f(
| λα+μβ |
| λ+μ |
| μα+λβ |
| λ+μ |
由(Ⅰ)可知,f(α)=
| 1 |
| α |
| 1 |
| β |
∴|f(α)-f(β)|=|
| 1 |
| α |
| 1 |
| β |
| β-α |
| αβ |
∴|f(
| λα+μβ |
| λ+μ |
| μα+λβ |
| λ+μ |
点评:本题考查的知识点是二次函数的图象和性质,函数的单调性的判断与证明,一元二次方程根与系数的关系(韦达定理),熟练掌握一元二次方程根与系数的关系(韦达定理)是解答的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
设集合A={x∈R|x+y=2},集合B={x∈R|x≤2},则A∩B=( )
| A、{2} | B、φ | C、A | D、B |
α,β,γ为不同的平面,m,n,l为不同的直线,则m⊥β的一个充分条件是( )
| A、n⊥α,n⊥β,m⊥α |
| B、α∩γ=m,α⊥γ,β⊥γ |
| C、α⊥γ,β⊥γ,m⊥α |
| D、α⊥β,α∩β=l,m⊥l |
cos2
-sin2
=( )
| π |
| 12 |
| π |
| 12 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
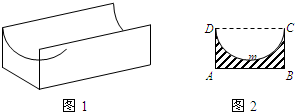 图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,示意图,其中四边形ABCD是矩形,弧CmD是半圆,凹槽的横截面的周长为4.设AB=2x,BC=y,凹槽的强度与横截面的面积的x倍成正比,且当AB=1时凹槽的强度为
图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,示意图,其中四边形ABCD是矩形,弧CmD是半圆,凹槽的横截面的周长为4.设AB=2x,BC=y,凹槽的强度与横截面的面积的x倍成正比,且当AB=1时凹槽的强度为