题目内容
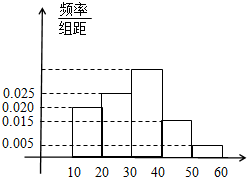 “你低碳了吗?”这是某市为倡导建设资源节约型社会而发布的公益广告里的一句话.活动组织者为了解这则广告的宣传效果,随机抽取了100名年龄段在[10,20),[20,30),…,[50,60)的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.
“你低碳了吗?”这是某市为倡导建设资源节约型社会而发布的公益广告里的一句话.活动组织者为了解这则广告的宣传效果,随机抽取了100名年龄段在[10,20),[20,30),…,[50,60)的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.(Ⅰ)求随机抽取的市民中年龄段在[30,40)的人数;
(Ⅱ)从不小于40岁的人中按年龄段分层抽样的方法随机抽取8人,求[50,60)年龄段抽取的人数;
(Ⅲ)从按(Ⅱ)中方式得到的8人中再抽取3人作为本次活动的获奖者,记X为年龄在[50,60)年龄段的人数,求X的分布列及数学期望.
考点:离散型随机变量的期望与方差,频率分布直方图
专题:概率与统计
分析:(Ⅰ)利用频率分布直方图能求出随机抽取的市民中年龄段在[30,40)的人数.
(Ⅱ)由频率公布直方图知100×0.15=15,100×0.05=5,由此能求出抽取的8人中[50,60)年龄段抽取的人数.
(Ⅲ)X的所有可能取值为0,1,2.分别求出相应的概率,由此能求出X的分布列和X的数学期望.
(Ⅱ)由频率公布直方图知100×0.15=15,100×0.05=5,由此能求出抽取的8人中[50,60)年龄段抽取的人数.
(Ⅲ)X的所有可能取值为0,1,2.分别求出相应的概率,由此能求出X的分布列和X的数学期望.
解答:
解:(Ⅰ)1-10×(0.020+0.025+0.015+0.005)=0.35,100×0.35=35,
即随机抽取的市民中年龄段在[30,40)的人数为35.…(4分)
(Ⅱ)100×0.15=15,100×0.05=5,
所以5×
=2,
即抽取的8人中[50,60)年龄段抽取的人数为2. …(7分)
(Ⅲ)X的所有可能取值为0,1,2.
P(X=0)=
=
;
P(X=1)=
=
;
P(X=2)=
=
.
所以X的分布列为
X的数学期望为EX=0×
+1×
+2×
=
.…(13分)
即随机抽取的市民中年龄段在[30,40)的人数为35.…(4分)
(Ⅱ)100×0.15=15,100×0.05=5,
所以5×
| 8 |
| 20 |
即抽取的8人中[50,60)年龄段抽取的人数为2. …(7分)
(Ⅲ)X的所有可能取值为0,1,2.
P(X=0)=
| ||
|
| 5 |
| 14 |
P(X=1)=
| ||||
|
| 15 |
| 28 |
P(X=2)=
| ||||
|
| 3 |
| 28 |
所以X的分布列为
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 5 |
| 14 |
| 15 |
| 28 |
| 3 |
| 28 |
| 3 |
| 4 |
点评:本题考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
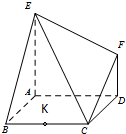 如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=
如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=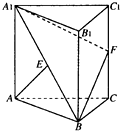 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为等边三角形,侧面AA1C1C是正方形,E是A1B的中点,F是棱CC1上的点.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为等边三角形,侧面AA1C1C是正方形,E是A1B的中点,F是棱CC1上的点.