题目内容
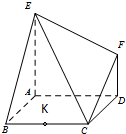 如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=
如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=| 1 |
| 2 |
(Ⅰ)求多面体EABCDF的体积;
(Ⅱ)求证:平面EAB⊥平面EBC;
(Ⅲ)记线段CB的中点为K,在平面ABCD内过K点作一条直线与平面ECF平行,要求保留作图痕迹,但不要求证明.
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)连接ED,由已知条件推导出FD⊥底面ABCD,AD⊥面FDC,由此能求出多面体EABCDF的体积.
(Ⅱ)由已知条件得AB⊥BC,BC⊥EA,从而得到BC⊥平面EAB,由此能证明平面EAB⊥平面EBC.
(Ⅲ)取线段DC的中点Q,连接KQ,直线KQ即为所求.
(Ⅱ)由已知条件得AB⊥BC,BC⊥EA,从而得到BC⊥平面EAB,由此能证明平面EAB⊥平面EBC.
(Ⅲ)取线段DC的中点Q,连接KQ,直线KQ即为所求.
解答:
(Ⅰ)解:如图,连接ED,
 ∵EA⊥底面ABCD,且FD∥EA,∴FD⊥底面ABCD,
∵EA⊥底面ABCD,且FD∥EA,∴FD⊥底面ABCD,
∴FD⊥AD,
∵DC⊥AD,FD∩CD=D,
∴AD⊥面FDC,…(1分)
∴VE-FCD=
AD•S△FDC=
×
×1×2×2=
,…(2分)
VE-ABCD=
EA•SABCD=
×2×2×2=
,(3分)
∴V多面体=VE-FCD+VE-ABCD=
.(5分)
(Ⅱ)证明:∵ABCD为正方形,∴AB⊥BC.(6分)
∵EA⊥平面ABCD,BC?平面ABCD,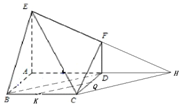
∴BC⊥EA.(7分)
又AB∩EA=A,∴BC⊥平面EAB.(8分)
又∵BC?平面EBC,
∴平面EAB⊥平面EBC.(10分)
(Ⅲ)解:取线段DC的中点Q,连接KQ,
则直线KQ即为所求.…(11分)
图上有正确的作图痕迹…(12分)
 ∵EA⊥底面ABCD,且FD∥EA,∴FD⊥底面ABCD,
∵EA⊥底面ABCD,且FD∥EA,∴FD⊥底面ABCD,∴FD⊥AD,
∵DC⊥AD,FD∩CD=D,
∴AD⊥面FDC,…(1分)
∴VE-FCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
VE-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 3 |
∴V多面体=VE-FCD+VE-ABCD=
| 10 |
| 3 |
(Ⅱ)证明:∵ABCD为正方形,∴AB⊥BC.(6分)
∵EA⊥平面ABCD,BC?平面ABCD,

∴BC⊥EA.(7分)
又AB∩EA=A,∴BC⊥平面EAB.(8分)
又∵BC?平面EBC,
∴平面EAB⊥平面EBC.(10分)
(Ⅲ)解:取线段DC的中点Q,连接KQ,
则直线KQ即为所求.…(11分)
图上有正确的作图痕迹…(12分)
点评:本题主要考查直线与直线,直线与平面,平面与平面位置关系等基础知识;考查空间想象能力,推理论证能力和运算求解能力.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
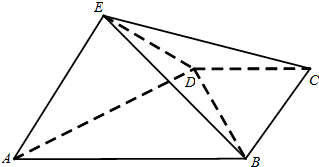 如图,四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.
如图,四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.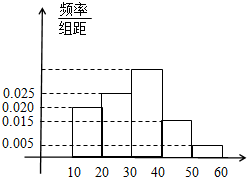 “你低碳了吗?”这是某市为倡导建设资源节约型社会而发布的公益广告里的一句话.活动组织者为了解这则广告的宣传效果,随机抽取了100名年龄段在[10,20),[20,30),…,[50,60)的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.
“你低碳了吗?”这是某市为倡导建设资源节约型社会而发布的公益广告里的一句话.活动组织者为了解这则广告的宣传效果,随机抽取了100名年龄段在[10,20),[20,30),…,[50,60)的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.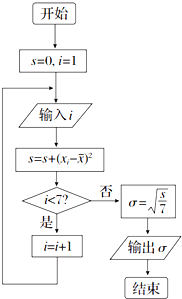 在2012~2013赛季NBA季后赛中,当一个球队进行完7场比赛被淘汰后,某个篮球爱好者对该队的7场比赛得分情况进行统计,如表:
在2012~2013赛季NBA季后赛中,当一个球队进行完7场比赛被淘汰后,某个篮球爱好者对该队的7场比赛得分情况进行统计,如表: