题目内容
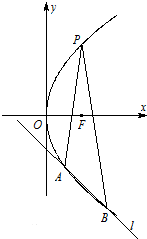
已知抛物线y2=2px(p>0)的焦点为F,点P是抛物线上的一点,且纵坐标为4,|PF|=4.
(1)求抛物线的方程;
(2)设直线l与抛物线交于A,B两点,且∠APB的角平分线与x轴垂直,求△PAB面积最大时直线l的方程.
(1)求抛物线的方程;
(2)设直线l与抛物线交于A,B两点,且∠APB的角平分线与x轴垂直,求△PAB面积最大时直线l的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设点P(x0,4),由已知条件得x0+
=4,42=2px0,由此能求出抛物线的方程为y2=8x.
(2)由(1)知点P的坐标为(2,4),由∠APB的角平分线与x轴垂直,知PA,PB的斜率互为相反数,设直线PA的方程为y-4=k(x-2),(k≠0)由
,得ky2-8y-16k+32=0,由此推导出可设直线AB的方程为y=-x+b,把x=-y+b代入抛物线方程得y2+8y-8b=0,从而能求出当b=0时,△PAB的面积取得最大值.此时直线l的方程为x+y=0.
| p |
| 2 |
(2)由(1)知点P的坐标为(2,4),由∠APB的角平分线与x轴垂直,知PA,PB的斜率互为相反数,设直线PA的方程为y-4=k(x-2),(k≠0)由
|
解答:
解:(1)设点P(x0,4),∵|PF|=4,
∴由抛物线的定义得x0+
=4.
 又∵42=2px0,二式联立解得x0=2,p=4.
又∵42=2px0,二式联立解得x0=2,p=4.
故此抛物线的方程为y2=8x.(4分)
(2)由(1)知点P的坐标为(2,4),
由∠APB的角平分线与x轴垂直,
知PA,PB的斜率互为相反数.(5分)
设直线PA的方程为y-4=k(x-2),(k≠0)
由
,消去x得ky2-8y-16k+32=0,
设A(x1,y1),B(x2,y2),则y1+4=
,即y1=
-4,
同理y2=-
-4.(7分)
∴直线AB的斜率为kAB=
=
=
=-1.(8分)
设直线AB的方程为y=-x+b,
把x=-y+b代入抛物线方程,得y2+8y-8b=0,
由题意知△=64+32b>0,且y1y2=-8b≥0,
从而-2<b≤0.又y1+y2=-8,
∴|AB|=
•|y1-y2|=8
,
点P到AB的距离d=
.
因此,S△PAB=2
•
,(10分)
令f(b)=(b+2)(b-6)2=b3-10b2+12b+72,(-2<b≤0),
则f'(b)=3b2-20b+12>0在b∈(-2,0]上恒成立,
∴函数f(b)在b∈(-2,0]上为增函数,
因此f(b)max=f(0)=72,
即△PAB面积的最大值为S△PAB=2
•
=24
∴当b=0时,△PAB的面积取得最大值.此时直线l的方程为x+y=0.(12分)
∴由抛物线的定义得x0+
| p |
| 2 |
 又∵42=2px0,二式联立解得x0=2,p=4.
又∵42=2px0,二式联立解得x0=2,p=4.故此抛物线的方程为y2=8x.(4分)
(2)由(1)知点P的坐标为(2,4),
由∠APB的角平分线与x轴垂直,
知PA,PB的斜率互为相反数.(5分)
设直线PA的方程为y-4=k(x-2),(k≠0)
由
|
设A(x1,y1),B(x2,y2),则y1+4=
| 8 |
| k |
| 8 |
| k |
同理y2=-
| 8 |
| k |
∴直线AB的斜率为kAB=
| y2-y1 |
| x2-x1 |
| 8(y2-y1) |
| y22-y12 |
| 8 |
| y1+y2 |
设直线AB的方程为y=-x+b,
把x=-y+b代入抛物线方程,得y2+8y-8b=0,
由题意知△=64+32b>0,且y1y2=-8b≥0,
从而-2<b≤0.又y1+y2=-8,
∴|AB|=
| 1+(-1)2 |
| b+2 |
点P到AB的距离d=
| |6-b| | ||
|
因此,S△PAB=2
| 2 |
| (b+2)(b-6)2 |
令f(b)=(b+2)(b-6)2=b3-10b2+12b+72,(-2<b≤0),
则f'(b)=3b2-20b+12>0在b∈(-2,0]上恒成立,
∴函数f(b)在b∈(-2,0]上为增函数,
因此f(b)max=f(0)=72,
即△PAB面积的最大值为S△PAB=2
| 2 |
| 72 |
∴当b=0时,△PAB的面积取得最大值.此时直线l的方程为x+y=0.(12分)
点评:本题考查抛物线方程的求法,考查三角形面积的最大值的求法,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目
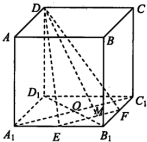 如图,在正方形ABCD=A1B1C1D1中,AB=2,O为底面正方形A1B1C1D1的中心,E、F分别为A1B1、B1C1的中点,点M为EF上一点,且满足
如图,在正方形ABCD=A1B1C1D1中,AB=2,O为底面正方形A1B1C1D1的中心,E、F分别为A1B1、B1C1的中点,点M为EF上一点,且满足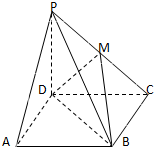 在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是正方形,若PD=DA,M是PC的中点.
在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是正方形,若PD=DA,M是PC的中点.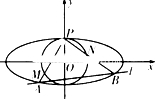 如图,椭圆C:
如图,椭圆C: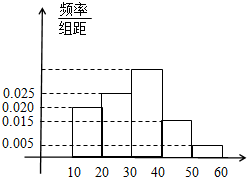 “你低碳了吗?”这是某市为倡导建设资源节约型社会而发布的公益广告里的一句话.活动组织者为了解这则广告的宣传效果,随机抽取了100名年龄段在[10,20),[20,30),…,[50,60)的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.
“你低碳了吗?”这是某市为倡导建设资源节约型社会而发布的公益广告里的一句话.活动组织者为了解这则广告的宣传效果,随机抽取了100名年龄段在[10,20),[20,30),…,[50,60)的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.