题目内容
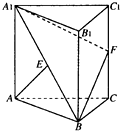 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为等边三角形,侧面AA1C1C是正方形,E是A1B的中点,F是棱CC1上的点.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为等边三角形,侧面AA1C1C是正方形,E是A1B的中点,F是棱CC1上的点.(1)若F是棱CC1中点时,求证:AE⊥平面A1FB;
(2)当VE-ABF=9
| 3 |
考点:直线与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)取AB的中点为M,连接EF,EM,CM,由已知条件推导出四边形EMCF是平行四边形,由AE⊥A1B,AE⊥A1B,能证明AE⊥平面A1FB.
(Ⅱ)设正方形AA1C1C的边长为x,由已知条件推导出点F到平面EAB的距离即为点C到平面平面AA1B的距离,由VE-EABF=VF-ABE,利用等积法能求出正方形的边长.
(Ⅱ)设正方形AA1C1C的边长为x,由已知条件推导出点F到平面EAB的距离即为点C到平面平面AA1B的距离,由VE-EABF=VF-ABE,利用等积法能求出正方形的边长.
解答:
解:(Ⅰ)取AB的中点为M,连接EF,EM,CM,
∵E是A1B的中点,F是棱CC1中点,
∴EM∥AA1,FC∥AA1,EM=FC=
AA1,
则四边形EMCF是平行四边形,∴EF∥CM,
 又∵△ABC为正三角形,侧面AA1C1C是正方形,
又∵△ABC为正三角形,侧面AA1C1C是正方形,
∴AA1=AB,∴AE⊥A1B,CM⊥AB,
∵侧棱AA1⊥平面ABC,∴CM⊥AA1,∴CM⊥平面A1AB,
∴EF⊥平面A1AB,∴EF⊥AE,
又∵AE⊥A1B,A1B∩EF=E,∴AE⊥平面A1FB.…(6分)
(Ⅱ)设正方形AA1C1C的边长为x,
由于E是A1B的中点,△EAB的面积为定值.
∵CC1∥平面AA1B,∴点F到平面EAB的距离为定值,
即为点C到平面平面AA1B的距离,
又VE-EABF=VF-ABE,且VF-ABE=
S△ABE•h=9
.
即
•
•x•
x=9
,解得x3=216,即x=6.
∴正方形的边长为6.…(12分)
∵E是A1B的中点,F是棱CC1中点,
∴EM∥AA1,FC∥AA1,EM=FC=
| 1 |
| 2 |
则四边形EMCF是平行四边形,∴EF∥CM,
 又∵△ABC为正三角形,侧面AA1C1C是正方形,
又∵△ABC为正三角形,侧面AA1C1C是正方形,∴AA1=AB,∴AE⊥A1B,CM⊥AB,
∵侧棱AA1⊥平面ABC,∴CM⊥AA1,∴CM⊥平面A1AB,
∴EF⊥平面A1AB,∴EF⊥AE,
又∵AE⊥A1B,A1B∩EF=E,∴AE⊥平面A1FB.…(6分)
(Ⅱ)设正方形AA1C1C的边长为x,
由于E是A1B的中点,△EAB的面积为定值.
∵CC1∥平面AA1B,∴点F到平面EAB的距离为定值,
即为点C到平面平面AA1B的距离,
又VE-EABF=VF-ABE,且VF-ABE=
| 1 |
| 3 |
| 3 |
即
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴正方形的边长为6.…(12分)
点评:本题考查直线与平面垂直的证明,考查正方形的边长的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
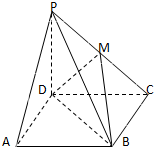 在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是正方形,若PD=DA,M是PC的中点.
在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是正方形,若PD=DA,M是PC的中点.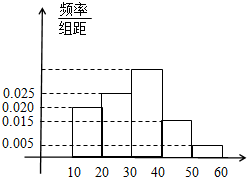 “你低碳了吗?”这是某市为倡导建设资源节约型社会而发布的公益广告里的一句话.活动组织者为了解这则广告的宣传效果,随机抽取了100名年龄段在[10,20),[20,30),…,[50,60)的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.
“你低碳了吗?”这是某市为倡导建设资源节约型社会而发布的公益广告里的一句话.活动组织者为了解这则广告的宣传效果,随机抽取了100名年龄段在[10,20),[20,30),…,[50,60)的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.