题目内容
设函数f(x)=x3-4x+a,0<a<2.若f(x)的三个零点为x1,x2,x3,且x1<x2<x3,有以下论断:
①x1>-1,
②x2<0,
③x2>0,
④x3>2.
其中正确的序号是 .(将你认为正确的论断的所有序号都填上)
①x1>-1,
②x2<0,
③x2>0,
④x3>2.
其中正确的序号是
考点:利用导数研究函数的极值,函数零点的判定定理
专题:函数的性质及应用,导数的综合应用
分析:利用导数研究函数的单调性,利用导数求函数的极值,再根据f (x)的三个零点为x1,x2,x3,且x1<x2<x3,求得各个零点所在的区间,结合特殊函数值f(0)、f(2)和a的范围,再判断出具体的零点范围.
解答:
解:∵函数f (x)=x3-4x+a,0<a<2,
∴f′(x)=3x2-4.
令f′(x)=0,可得 x=±
,
当x<-
或x>
时,f′(x)>0;
当-
<x<
时,f′(x)<0;
故函数在(-∞,-
)、(
,+∞)上是增函数,在(-
,
)上是减函数,
故f(-
)是极大值,f(
)是极小值,
再由f(x)的三个零点为x1,x2,x3,且x1<x2<x3,
可得 x1<-
<x2<
<x3,
根据f(0)=f(2)=a>0,且f(
)=a-
<0,
可得0<x2<
,
<x3<2,
即x1<-
<-1,故①不正确;0<x2<
,故②不正确,③正确;
<x3<2,故④不正确.
故答案为:③.
∴f′(x)=3x2-4.
令f′(x)=0,可得 x=±
2
| ||
| 3 |
当x<-
2
| ||
| 3 |
2
| ||
| 3 |
当-
2
| ||
| 3 |
2
| ||
| 3 |
故函数在(-∞,-
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
故f(-
2
| ||
| 3 |
2
| ||
| 3 |
再由f(x)的三个零点为x1,x2,x3,且x1<x2<x3,
可得 x1<-
2
| ||
| 3 |
2
| ||
| 3 |
根据f(0)=f(2)=a>0,且f(
2
| ||
| 3 |
16
| ||
| 9 |
可得0<x2<
2
| ||
| 3 |
2
| ||
| 3 |
即x1<-
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
故答案为:③.
点评:本题主要考查函数的零点的定义,函数的零点与方程的根的关系,利用导数研究函数的单调性,利用导数求函数的极值,属于中档题.

练习册系列答案
相关题目
设随机变量X~N(μ,σ2),则η=ax+b服从( )
| A、N(μ,σ2) | ||||
| B、N(aμ+b,a2σ2) | ||||
| C、N(0,1) | ||||
D、N(
|
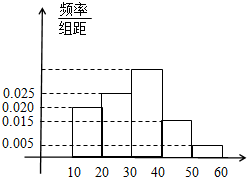 “你低碳了吗?”这是某市为倡导建设资源节约型社会而发布的公益广告里的一句话.活动组织者为了解这则广告的宣传效果,随机抽取了100名年龄段在[10,20),[20,30),…,[50,60)的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.
“你低碳了吗?”这是某市为倡导建设资源节约型社会而发布的公益广告里的一句话.活动组织者为了解这则广告的宣传效果,随机抽取了100名年龄段在[10,20),[20,30),…,[50,60)的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.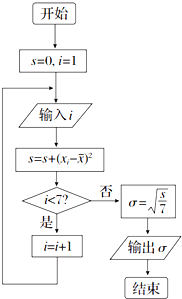 在2012~2013赛季NBA季后赛中,当一个球队进行完7场比赛被淘汰后,某个篮球爱好者对该队的7场比赛得分情况进行统计,如表:
在2012~2013赛季NBA季后赛中,当一个球队进行完7场比赛被淘汰后,某个篮球爱好者对该队的7场比赛得分情况进行统计,如表: