题目内容
8.已知直线y=a(0<a<1)与函数f(x)=sinωx在y轴右侧的前12个交点横坐标依次为x1,x2,x3,…,x12,且x1=$\frac{π}{4}$,x2=$\frac{3π}{4}$,x3=$\frac{9π}{4}$,则x1+x2+x3+…+x12=66π.分析 由题意,函数的周期为2π,ω=1,f(x)=sinx,a=$\frac{\sqrt{2}}{2}$,根据对称性,即可得出结论.
解答 解:由题意,函数的周期为2π,ω=1,f(x)=sinx,a=$\frac{\sqrt{2}}{2}$,
∴x1+x2+x3+…+x12=π+5π+9π+13π+17π+21π=66π.
故答案为66π.
点评 本题考查三角函数的图象与性质,考查对称性,属于中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
16.已知全集U={1,2,3,4,5,6,7},A={2,4,5},B={1,3,5,7},则A∩(∁UB)为( )
| A. | {1,4,6} | B. | {2,4,6} | C. | {2,4} | D. | {4} |
3.要得到y=sin$\frac{x}{2}$的图象,只需将y=cos($\frac{x}{2}$-$\frac{π}{4}$)的图象上的所有点( )
| A. | 向右平移$\frac{π}{2}$ | B. | 向左平移$\frac{π}{2}$ | C. | 向左平移$\frac{π}{4}$ | D. | 向右平移$\frac{π}{4}$ |
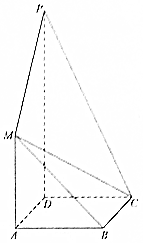 如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.
如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.