题目内容
18.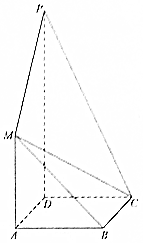 如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.
如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.(1)求证:MB∥平面PDC;
(2)求二面角M-PC-D的余弦值.
分析 (1)推导出AB∥CD,MA∥PD,从而平面ABM∥平面PDC,由此能证明MB∥平面PDC.
(2)推导出CD⊥PD,AD⊥PD,AD⊥DC,以DA为x轴,DC为y轴,DP为z轴建立空间直角坐标系,利用向量法能求出二面角M-PC-D的余弦值.
解答 (本小题满分12分)
证明:(1)∵四边形ABCD是正方形,∴AB∥CD,
又∵MA∥PD,…(1分)
AB∩MA=A,CD∩PD=D,
AB?平面ABM,MA?平面ABM,CD?平面PDC,PD?平面PDC,
∴平面ABM∥平面PDC,(3分)
∵MB?平面ABM,
∴MB∥平面PDC.(4分)
解:(2)∵正方形ABCD与梯形AMPD所在的平面互相垂直,
平面ABCD∩平面AMPD=AD,在正方形ABCD中,CD⊥AD,
∴CD⊥平面AMPD,∴CD⊥PD.(6分)
又AD⊥PD,AD⊥DC,
以DA为x轴,DC为y轴,DP为z轴建立空间直角坐标系,(7分)
则M(1,0,1),P(0,0,2),C(0,1,0),
$\overrightarrow{DA}=(1,0,0)$是平面PCD的一个法向量
设平面MPC的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PM}=x-z=0}\\{\overrightarrow{n}•\overrightarrow{CM}=x-y+z=0}\end{array}\right.$,(9分)
令z=1,得$\overrightarrow{n}$=(1,2,1),(10分)
则cos<$\overrightarrow{DA},\overrightarrow{n}$>=$\frac{\overrightarrow{DA}•\overrightarrow{n}}{|\overrightarrow{DA}|•|\overrightarrow{n}|}$=$\frac{1}{\sqrt{6}}=\frac{\sqrt{6}}{6}$,(11分)
设二面角M-PC-D为θ,由图可知θ为锐角,
所以二面角M-PC-D的余弦值为$\frac{\sqrt{6}}{6}$.(12分)
点评 本题考查线面平行的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | 0 | B. | ±3 | C. | 3 | D. | -3 |
| A. | g(x)是奇函数 | B. | g(x)的图象关于直线x=-$\frac{π}{4}$对称 | ||
| C. | g(x)在[$\frac{π}{4}$,$\frac{π}{2}$]上的增函数 | D. | 当x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,g(x)的值域是[-2,1] |
| A. | ?x0∈R,x03-x02+1<0 | B. | ?x∈R,x3-x2+1≤0 | ||
| C. | ?x0∈R,x03-x02+1≤0 | D. | ?x∈R,x3-x2+1>0 |
 如图是某几何体的三视图,其正视图、俯视图均为直径为2的半圆,则该几何体的表面积为( )
如图是某几何体的三视图,其正视图、俯视图均为直径为2的半圆,则该几何体的表面积为( )| A. | 3π | B. | 4π | C. | 5π | D. | 12π |
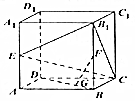 如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.
如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.