题目内容
3.要得到y=sin$\frac{x}{2}$的图象,只需将y=cos($\frac{x}{2}$-$\frac{π}{4}$)的图象上的所有点( )| A. | 向右平移$\frac{π}{2}$ | B. | 向左平移$\frac{π}{2}$ | C. | 向左平移$\frac{π}{4}$ | D. | 向右平移$\frac{π}{4}$ |
分析 利用诱导公式,函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:将y=cos($\frac{x}{2}$-$\frac{π}{4}$)的图象上的所有点向右平移$\frac{π}{2}$个单位,
可得y=cos($\frac{x-\frac{π}{2}}{2}$-$\frac{π}{4}$)=cos($\frac{x}{2}$-$\frac{π}{2}$)=sin$\frac{x}{2}$的图象,
故选:A.
点评 本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
13.命题“?x0∈R,x03-x02+1>0”的否定是( )
| A. | ?x0∈R,x03-x02+1<0 | B. | ?x∈R,x3-x2+1≤0 | ||
| C. | ?x0∈R,x03-x02+1≤0 | D. | ?x∈R,x3-x2+1>0 |
11.设函数f(x)=$\left\{\begin{array}{l}{x-2,x≥1}\\{2,x<1}\end{array}\right.$,则满足xf(x-1)≥10的x取值范围为[5,+∞).
18.用二分法研究函数f(x)=x3-2x-1的理念时,若零点所在的初始区间为(1,2),则下一个有解区间为( )
| A. | (1,2) | B. | (1.75,2) | C. | (1.5,2) | D. | (1,1.5) |
12.“x>-2”是“(x+2)(x-3)<0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
13.命题p:“?x∈R,x2+2<0”,则¬p为( )
| A. | ?x∈R,x2+2≥0 | B. | ?x∉R,x2+2<0 | C. | ?x∈R,x2+2≥0 | D. | ?x∈R,x2+2>0 |
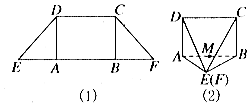 如图所示,在等腰梯形CDEF中,DE=CD=$\sqrt{2}$,EF=2+$\sqrt{2}$,将它沿着两条高AD,CB折叠成如图(2)所示的四棱锥E-ABCD(E,F重合).
如图所示,在等腰梯形CDEF中,DE=CD=$\sqrt{2}$,EF=2+$\sqrt{2}$,将它沿着两条高AD,CB折叠成如图(2)所示的四棱锥E-ABCD(E,F重合).