题目内容
18．已知命题p：$\frac{{x}^{2}}{3-a}-\frac{{y}^{2}}{a-5}=1$可表示焦点在x轴上的双曲线；命题q：若实数a，b满足a＞b，则a2＞b2．则下列命题中：①p∨q②p∧q③（￢p）∨q④（￢p）∧（￢q）真命题的序号为（ ）| A． | ① | B． | ③④ | C． | ①③ | D． | ①②③ |
分析 先分别判定命题p、命题q的真假，在根据复合命题的真值表判定．
解答 解：对于命题p：若$\frac{{x}^{2}}{3-a}-\frac{{y}^{2}}{a-5}=1$可表示焦点在x轴上的双曲线，则3-a＞0，a-5＞0，a不存在，故命题p是假命题；
对于命题q：若实数a，b满足a＞b，则a2＞b2或a2=b2或a2＜b2，命题q为假命题；
①p∨q为假，②p∧q为假，③（￢p）∨q为真，④（￢p）∧（￢q）为真；
故选：B．
点评 本题考查了命题真假的判定，涉及到了圆锥曲线和不等式的性质，属于基础题．
练习册系列答案
导学教程高中新课标系列答案
相关题目
9．在空间中，下列命题中不正确的是（ ）
| A． | 若两个平面有一个公共点，则它们有无数个公共点 | |
| B． | 任意两条直线能确定一个平面 | |
| C． | 若点A既在平面α内，又在平面β内，则α与β相交于直线b，且点A在直线b上 | |
| D． | 若已知四个点不共面，则其中任意三点不共线 |
6．已知抛物线C的顶点在原点，焦点为F（-3，0），C上一点P到焦点F的距离为9，则点P的一个坐标为（ ）
| A． | （-3，6） | B． | （-3，6$\sqrt{2}$） | C． | （-6，6） | D． | （-6，6$\sqrt{2}$） |
13．命题p：“?x∈R，x2+2＜0”，则￢p为（ ）
| A． | ?x∈R，x2+2≥0 | B． | ?x∉R，x2+2＜0 | C． | ?x∈R，x2+2≥0 | D． | ?x∈R，x2+2＞0 |
10．
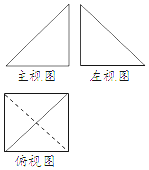如图，某几何体的主视图和左视图是全等的等腰直角三角形，俯视图是边长为2的正方形，那么它的体积为（ ）
如图，某几何体的主视图和左视图是全等的等腰直角三角形，俯视图是边长为2的正方形，那么它的体积为（ ）| A． | $\frac{16}{3}$ | B． | 4 | C． | $\frac{8}{3}$ | D． | $\frac{4}{3}$ |