题目内容
 在空间直角坐标系中,已知O (0,0,0),A(2,-1,3),B(2,1,1).
在空间直角坐标系中,已知O (0,0,0),A(2,-1,3),B(2,1,1).(1)求|AB|的长度;
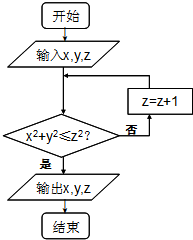
(2)写出A、B两点经此程序框图执行运算后的对应点A0,B0的坐标,并说出点A0,B0在空间直角坐标系o-xyz中的关系.
考点:程序框图
专题:算法和程序框图
分析:(1)由已知中A,B两点的坐标,代入空间两点间距离公式,可得答案.
(2)将已知中A,B两点的坐标,代入算法,求出对应点A0,B0的坐标,可得结论.
(2)将已知中A,B两点的坐标,代入算法,求出对应点A0,B0的坐标,可得结论.
解答:
解:(1)∵A(2,-1,3),B(2,1,1).
∴|AB|=
=2
(2)∵A(2,-1,3)满足 22+(-1)2≤32
∴输出A0(2,-1,3)
∵B(2,1,1)不满足22+12≤12
∴z=z+1=2
∵(2,1,2)不满足22+12≤22
∴z=z+1=3
∵(2,1,3)满足22+12≤32
∴输出B0(2,1,3)
∴A0,B0关于平面xoz对称
∴|AB|=
| (2-2)2+(-1-1)2+(3-1)2 |
| 2 |
(2)∵A(2,-1,3)满足 22+(-1)2≤32
∴输出A0(2,-1,3)
∵B(2,1,1)不满足22+12≤12
∴z=z+1=2
∵(2,1,2)不满足22+12≤22
∴z=z+1=3
∵(2,1,3)满足22+12≤32
∴输出B0(2,1,3)
∴A0,B0关于平面xoz对称
点评:本题考查的知识点是程序框图,空间两点之间距离公式,难度不大,属于基础题.

练习册系列答案
相关题目
下列函数中,既是偶函数,又在区间(0,+∞)上单调递减的函数为( )
| A、f(x)=x-1 | ||
| B、f(x)=cosx | ||
| C、f(x)=2|x| | ||
D、f(x)=log
|
若直线mx-y+2=0与圆x2+y2=1只有一个交点,则实数m的值是( )
| A、±1 | ||
B、±
| ||
C、±
| ||
| D、±2 |
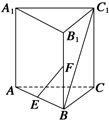 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1的夹角是
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1的夹角是