题目内容
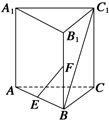如图所示，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，AB=BC=AA1，∠ABC=90°，点E、F分别是棱AB、BB1的中点，则直线EF和BC1的夹角是考点：用空间向量求直线间的夹角、距离,异面直线及其所成的角
专题：空间角,空间向量及应用
分析：通过建立空间直角坐标系，利用向量的夹角公式即可得出．
解答：
解：如图所示，建立空间直角坐标系．
由于AB=BC=AA1，不妨取AB=2，
则E（0，1，0），F（0，0，1），C1（2，0，2）．
∴
=（0，-1，1），
=（2，0，2）．
∴cos＜
，
＞=
=
=
．
∴异面直线EF和BC1的夹角为
．
故答案为：
．
由于AB=BC=AA1，不妨取AB=2，
则E（0，1，0），F（0，0，1），C1（2，0，2）．
∴
| EF |
| BC1 |
∴cos＜
| EF |
| BC1 |
| ||||
|
|
| 2 | ||||
|
| 1 |
| 2 |
∴异面直线EF和BC1的夹角为
| π |
| 3 |
故答案为：
| π |
| 3 |
点评：本题考查了通过建立空间直角坐标系和向量的夹角公式求异面直线的夹角，属于基础题．
练习册系列答案
相关题目
直线在平面外是指（ ）
| A、直线与平面没有公共点 |
| B、直线与平面相交 |
| C、直线与平面平行 |
| D、直线与平面最多只有一个公共点 |
在空间直角坐标系中，已知O （0，0，0），A（2，-1，3），B（2，1，1）．已知△ABC三个顶点在同一个球面上，∠BAC=90°，AB=AC=2，若球心到平面ABC距离为1，则该球体积为（ ）
A、2
| ||
B、4
| ||
C、6
| ||
D、8
|
不等式组
的解在数轴上表示为（ ）
|
A、 |
B、 |
C、 |
D、 |