题目内容
某大街在甲、乙、丙三处设有红绿灯,汽车在这三处因绿灯而通行的概率分别为
,
,
,则汽车在这三处因遇红灯而停车一次的概率为( )
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:分别求得仅在甲处因遇红灯而停车的概率,仅在乙处因遇红灯而停车的概率,仅在丙处因遇红灯而停车的概率,
相加即得所求.
相加即得所求.
解答:
解:仅在甲处因遇红灯而停车的概率为
×
×
=
,
仅在乙处因遇红灯而停车的概率为
×
×
=
,
仅在丙处因遇红灯而停车的概率为
×
×
=
,
故汽车在这三处因遇红灯而停车一次的概率为
+
+
=
,
故选:D.
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 9 |
仅在乙处因遇红灯而停车的概率为
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 9 |
仅在丙处因遇红灯而停车的概率为
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 18 |
故汽车在这三处因遇红灯而停车一次的概率为
| 2 |
| 9 |
| 1 |
| 9 |
| 1 |
| 18 |
| 7 |
| 18 |
故选:D.
点评:本题主要考查相互独立事件的概率乘法公式,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
设全集U=R,集合A={x|x+1>0},B={x|y=ln(1-x)},则A∩(∁RB)=( )
| A、{x|-1<x<1} |
| B、{x|x≥1} |
| C、{x|x>-1} |
| D、以上都不对 |
已知复数z1=2-2i,z2在复平面内对应的点在直线x=1上,且满足z1•z2是实数,则z2等于( )
| A、1-i | B、1+i |
| C、+i | D、-i |
下列说法一定正确的是( )
| A、直角三角形绕其一边旋转形成圆锥 |
| B、等边三角形绕其一边旋转形成圆锥 |
| C、平面截圆锥所得的图形是圆 |
| D、过圆锥顶点的截面图形是等腰三角形 |
若{an}为等差数列,Sn是其前n项和,且S13=
π,则tana7的值为( )
| 13 |
| 4 |
| A、-1 | ||||
B、-
| ||||
C、±
| ||||
| D、1 |
给出下列说法:
①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;
②用相关指数可以刻画回归的效果,值越小说明模型的拟合效果越好;
③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型拟合效果越好.
其中正确的是( )
①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;
②用相关指数可以刻画回归的效果,值越小说明模型的拟合效果越好;
③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型拟合效果越好.
其中正确的是( )
| A、①② | B、②③ | C、①③ | D、①②③ |
已知条件p:α是两条直线的夹角,条件q:α是第一象限的角.则“条件p”是“条件q”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
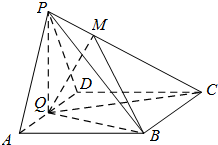 如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,平面PAD⊥平面ABCD,PA=PD=AD=2,Q为AD的中点,M是棱PC上一点,且PM=
如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,平面PAD⊥平面ABCD,PA=PD=AD=2,Q为AD的中点,M是棱PC上一点,且PM=