题目内容
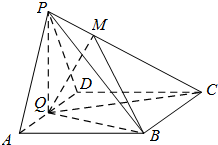 如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,平面PAD⊥平面ABCD,PA=PD=AD=2,Q为AD的中点,M是棱PC上一点,且PM=
如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,平面PAD⊥平面ABCD,PA=PD=AD=2,Q为AD的中点,M是棱PC上一点,且PM=| 1 |
| 3 |
(Ⅰ)求证:PQ⊥平面ABCD;
(Ⅱ)证明:PA∥平面BMQ;
(Ⅲ)求二面角M-BQ-C的度数.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定,直线与平面垂直的判定
专题:空间角
分析:(1)根据已知中平面PAD⊥平面ABCD,结合面面垂直的性质定理,易得PQ⊥平面ABCD;
(2)证明线面平行,关键是利用线面平行的判定定理,只要证明PA平行于平面内的一条直线;
(3)连结BD,以Q为坐标原点,QA,QB,QP分别为x轴y轴z轴建立空间直角坐标系,求出平面BMQ和BCQ的法向量,代入向量夹角公式,可得答案.
(2)证明线面平行,关键是利用线面平行的判定定理,只要证明PA平行于平面内的一条直线;
(3)连结BD,以Q为坐标原点,QA,QB,QP分别为x轴y轴z轴建立空间直角坐标系,求出平面BMQ和BCQ的法向量,代入向量夹角公式,可得答案.
解答:
证明:(I)由已知中PA=PD,Q为AD的中点,
∴PQ⊥AD,
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ?平面PAD,
∴PQ⊥平面ABCD;
(Ⅱ)连接AC交BQ于N,连接MN,
∵AQ∥BC,
∴△ANQ∽△CNB
∴
=
=
,
∴
=
,
∵PM=
PC,
∴PA∥MN
∵PA?平面MQB,MN?平面MQB
∴PA∥平面MQB
(Ⅲ)连结BD,∵底面ABCD是菱形,且∠BAD=60°,
∴△BAD是等边三角形,
∴BQ⊥AD由(Ⅰ)PQ⊥平面ABCD.
∴PQ⊥AD.
以Q为坐标原点,QA,QB,QP分别为x轴y轴z轴建立空间直角坐标系
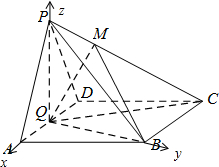
则Q(0,0,0),A(1,0,0),B(0,
,0),P(0,0,
).
设平面BMQ的法向量为
=(x,y,z),
∴
,注意到MN∥PA
∴
,
解得
=(
,0,1)是平面BMQ的一个法向量
又∵平面BCQ的法向量为
=
=(0,0,
)
故二面角M-BQ-C的平面角θ满足:
cosθ=
=
,
故θ=
,
即二面角M-BQ-C的平面角为
.
∴PQ⊥AD,
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ?平面PAD,
∴PQ⊥平面ABCD;
(Ⅱ)连接AC交BQ于N,连接MN,
∵AQ∥BC,
∴△ANQ∽△CNB
∴
| AQ |
| BC |
| AN |
| NC |
| 1 |
| 2 |
∴
| AN |
| AC |
| 1 |
| 3 |
∵PM=
| 1 |
| 3 |
∴PA∥MN
∵PA?平面MQB,MN?平面MQB
∴PA∥平面MQB
(Ⅲ)连结BD,∵底面ABCD是菱形,且∠BAD=60°,
∴△BAD是等边三角形,
∴BQ⊥AD由(Ⅰ)PQ⊥平面ABCD.
∴PQ⊥AD.
以Q为坐标原点,QA,QB,QP分别为x轴y轴z轴建立空间直角坐标系

则Q(0,0,0),A(1,0,0),B(0,
| 3 |
| 3 |
设平面BMQ的法向量为
| m |
∴
|
∴
|
解得
| m |
| 3 |
又∵平面BCQ的法向量为
| n |
| QP |
| 3 |
故二面角M-BQ-C的平面角θ满足:
cosθ=
|
| ||||
|
|
| 1 |
| 2 |
故θ=
| π |
| 3 |
即二面角M-BQ-C的平面角为
| π |
| 3 |
点评:本题考查线面平行,考查面面角,解题的关键是利用线面平行的判定,理解面面角的定义,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
若复数z满足(z+2)i=5+5i(i为虚数单位),则z为( )
| A、3+5i | B、3-5i |
| C、-3+5i | D、-3-5i |
某大街在甲、乙、丙三处设有红绿灯,汽车在这三处因绿灯而通行的概率分别为
,
,
,则汽车在这三处因遇红灯而停车一次的概率为( )
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)是奇函数,且f(x+2)=-f(x),若f(x)在[-1,0]上是增函数,f(1),f(
),f(
)的大小关系是( )
| 3 |
| 2 |
| 13 |
| 3 |
A、f(1)<f(
| ||||
B、f(
| ||||
C、f(
| ||||
D、f(
|