题目内容
下列说法一定正确的是（ ）
| A、直角三角形绕其一边旋转形成圆锥 |
| B、等边三角形绕其一边旋转形成圆锥 |
| C、平面截圆锥所得的图形是圆 |
| D、过圆锥顶点的截面图形是等腰三角形 |
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：根据圆锥的几何特征及定义，分析四个答案的正误，可得结论．
解答：
解：直角三角形绕其斜边旋转形成的是两个圆锥形成的组合体，故A错误；
等边三角形绕其一边旋转形成的是两个圆锥形成的组合体，故B错误；
平面截圆锥所得的图形是圆或椭圆或抛物线或双曲线的一支，故C错误；
圆锥的母线均相等，故过圆锥顶点的截面图形是等腰三角形，故D正确；
故选D
等边三角形绕其一边旋转形成的是两个圆锥形成的组合体，故B错误；
平面截圆锥所得的图形是圆或椭圆或抛物线或双曲线的一支，故C错误；
圆锥的母线均相等，故过圆锥顶点的截面图形是等腰三角形，故D正确；
故选D
点评：本题考查的知识点是旋转体，熟练掌握圆锥的几何特征是解答的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
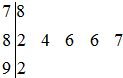如图是2010年元旦晚会举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的方差为（ ）| A、4.84 | B、0.8 |
| C、1.6 | D、3.2 |
若复数z满足（z+2）i=5+5i（i为虚数单位），则z为（ ）
| A、3+5i | B、3-5i |
| C、-3+5i | D、-3-5i |
将51转化为二进制数得（ ）
| A、100111（2） |
| B、110011（2） |
| C、110110（2） |
| D、110101（2） |
若2m+2n＜4，则点（m，n）必在（ ）
| A、直线x+y-2=0的左下方 |
| B、直线x+y-2=0的右上方 |
| C、直线x+2y-2=0的右上方 |
| D、直线x+2y-2=0的左下方 |
若（
-x
）n展开式中含有x2项，则n的最小值是（ ）
| 1 |
| x |
| x |
| A、15 | B、8 | C、7 | D、3 |
某大街在甲、乙、丙三处设有红绿灯，汽车在这三处因绿灯而通行的概率分别为
，
，
，则汽车在这三处因遇红灯而停车一次的概率为（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）是奇函数，且f（x+2）=-f（x），若f（x）在[-1，0]上是增函数，f(1)，f(
)，f(
)的大小关系是（ ）
| 3 |
| 2 |
| 13 |
| 3 |
A、f(1)＜f(
| ||||
B、f(
| ||||
C、f(
| ||||
D、f(
|