题目内容
圆锥底面半径为2,其母线与底面所成的角为60°,则它的侧面积为 .
考点:棱柱、棱锥、棱台的侧面积和表面积
专题:空间位置关系与距离
分析:根据圆锥的底面半径为2,母线与底面所成的角为60°求出母线的长,把圆锥沿着母线PA剪开后再展开,得到一个以PA为半径,以圆锥底面圆的周长为弧长的扇形,则展开后扇形的面积即为圆锥的侧面积.
解答:
解:如图,
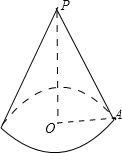
O为圆锥底面圆的圆心,圆锥的底面半径OA=2,母线PA与底面所成的角为∠PAO=60°,
则PA=4,
该圆锥的侧面展开图为以PA为半径,以圆锥底面圆的周长为弧长的扇形,
如图,
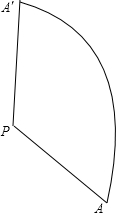
则展开后扇形的弧长l=2π•OA=4π,
所以,展开后扇形的面积为S=
•l•PA=
•4π•4=8π
即圆锥的侧面积为8π.
故答案为8π.

O为圆锥底面圆的圆心,圆锥的底面半径OA=2,母线PA与底面所成的角为∠PAO=60°,
则PA=4,
该圆锥的侧面展开图为以PA为半径,以圆锥底面圆的周长为弧长的扇形,
如图,

则展开后扇形的弧长l=2π•OA=4π,
所以,展开后扇形的面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
即圆锥的侧面积为8π.
故答案为8π.
点评:本题考查了圆锥的侧面积的求法,圆锥的侧面积就是把圆锥沿着一条母线剪开后再展开得到的扇形面积,圆锥的母线是所得扇形的半径,圆锥的底面圆的周长是所得扇形的弧长,另外对于扇形面积公式的记忆可模仿三角形面积公式的记法,此题是中低档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数列{an}的通项公式为an=2n+4n-2,则数列{an}的前n项和sn=( )
| A、2n+2n2-1 |
| B、2n+2n2-2 |
| C、2n+1+2n2-1 |
| D、2n+1+2n2-2 |
设x、y满足约束条件
,若x2+y2≥a恒成立,则实数a的最大值为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知变量x,y满足约束条件
,则z=4x+y的最小值为( )
|
| A、55 | B、-55 | C、5 | D、-5 |