题目内容
已知数列{an}中,a1=1,当n≥2,n∈N*时,an=3an-1-1,数列{bn}的前n项和Sn满足Sn=2n2+2n-2,n∈N*.(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)若cn=(an-
)•bn(n∈N*),求数列{cn}的前n项和Tn.
(Ⅱ)若cn=(an-
| 1 |
| 2 |
考点:数列的求和,等差数列的通项公式,等比数列的通项公式
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件,利用构造法能求出{an-
}是首项为
,公比为3的等比数列,由此能求出{an}的通项公式.利用bn=
,能求出{bn}的通项公式.
(Ⅱ)由cn=(an-
)•bn=
,利用错位相减法能求出数列{cn}的前n项和Tn.
| 1 |
| 2 |
| 1 |
| 2 |
|
(Ⅱ)由cn=(an-
| 1 |
| 2 |
|
解答:
解:(Ⅰ)数列{an}中,
∵a1=1,当n≥2,n∈N*时,an=3an-1-1,
an-
=3(an-1-
),a1-
=
,
∴{an-
}是首项为
,公比为3的等比数列,
∴an-
=
•3n-1,
∴an=
.…(3分)
∵数列{bn}的前n项和Sn满足Sn=2n2+2n-2,n∈N*,
∴b1=S1=2,
当n≥2时,bn=Sn-Sn-1=(2n2+2n-2)-[2(n-1)2+2(n-1)-2]=4n,
∴bn=
.…(6分)
(Ⅱ)∵an=
,bn=
,
∴cn=(an-
)•bn
=
•bn=
,
∴Tn=1+4•3+6•32+8•33+…+2n•3n-1,①
3Tn=3+4•32+6•33+8•34+…+2n•3n,②
①-②,得:-2Tn=-2+12+2(32+33+…+3n-1)-2n•3n
=10+2×
-2n•3n
=10+3n-9-2n•3n
=1+(1-2n)•3n,
∴Tn=
,n∈N*.…(12分)
∵a1=1,当n≥2,n∈N*时,an=3an-1-1,
an-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴{an-
| 1 |
| 2 |
| 1 |
| 2 |
∴an-
| 1 |
| 2 |
| 1 |
| 2 |
∴an=
| 3n-1 +1 |
| 2 |
∵数列{bn}的前n项和Sn满足Sn=2n2+2n-2,n∈N*,
∴b1=S1=2,
当n≥2时,bn=Sn-Sn-1=(2n2+2n-2)-[2(n-1)2+2(n-1)-2]=4n,
∴bn=
|
(Ⅱ)∵an=
| 3n-1 +1 |
| 2 |
|
∴cn=(an-
| 1 |
| 2 |
=
| 3n-1 |
| 2 |
|
∴Tn=1+4•3+6•32+8•33+…+2n•3n-1,①
3Tn=3+4•32+6•33+8•34+…+2n•3n,②
①-②,得:-2Tn=-2+12+2(32+33+…+3n-1)-2n•3n
=10+2×
| 9(1-3n-2) |
| 1-3 |
=10+3n-9-2n•3n
=1+(1-2n)•3n,
∴Tn=
| (2n-1)•3n-1 |
| 2 |
点评:本题考查数列的通项公式和前n项和公式的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
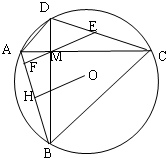 如图,四边形ACBD内接于圆O,对角线AC与BD相交于M,AC⊥BD,E是DC中点连结EM交AB于F,作OH⊥AB于H,求证:
如图,四边形ACBD内接于圆O,对角线AC与BD相交于M,AC⊥BD,E是DC中点连结EM交AB于F,作OH⊥AB于H,求证: