题目内容
设有两个命题：①方程x2+ax+9=0没有实数根；②实数a为非负数．如果这两个命题中有且只有一个是真命题，那么实数a的取值范围是 ．
考点：命题的真假判断与应用
专题：简易逻辑
分析：利用分析没有实数根求出①中a的范围，结合②a的范围，画出数轴即可求出结果．
解答：
解：：①方程x2+ax+9=0没有实数根；则△=a2-36＜0，解得-6＜a＜6；
②实数a为非负数，即a≥0；数轴表示出两个命题中a的范围如图：
如果这两个命题中有且只有一个是真命题，∴a∈（-6，0）∪[6，+∞）．
故答案为：（-6，0）∪[6，+∞）．
解：：①方程x2+ax+9=0没有实数根；则△=a2-36＜0，解得-6＜a＜6；②实数a为非负数，即a≥0；数轴表示出两个命题中a的范围如图：
如果这两个命题中有且只有一个是真命题，∴a∈（-6，0）∪[6，+∞）．
故答案为：（-6，0）∪[6，+∞）．
点评：本题考查命题真假的判断，复合命题真假的应用，集合的交、并、补的混合运算，基本知识的考查．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
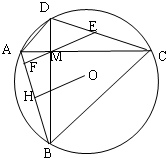如图，四边形ACBD内接于圆O，对角线AC与BD相交于M，AC⊥BD，E是DC中点连结EM交AB于F，作OH⊥AB于H，求证：
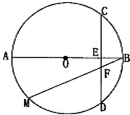如图，AB为半径为2的圆O的直径，CD为垂直于AB的一条弦，垂足为E，弦BM与CD交于点F．则AC2+BF•BM=