题目内容
在数列{an}中,a1=1,an+2+(-1)nan=2,记Sn是数列{an}的前n项和,则S60= .
考点:数列的求和
专题:等差数列与等比数列
分析:由an+2+(-1)nan=2得,当n为奇数时,an+2-an=2,数列{an}的奇数项构成等差数列,当n为偶数时,an+2+an=2,由此利用分组求和法能求出S60.
解答:
解:由an+2+(-1)nan=2得,
当n为奇数时,an+2-an=2,
即数列{an}的奇数项构成等差数列,首项为1,公差为2,
当n为偶数时,an+2+an=2,
即a2+a4=a4+a6=…=2,
∴S60=(a1+a3+…+a59)+(a2+a4+…+a60)
=(1+3+…)+(2+2+…)
=30×1+
+2×15=930,
故答案为:930.
当n为奇数时,an+2-an=2,
即数列{an}的奇数项构成等差数列,首项为1,公差为2,
当n为偶数时,an+2+an=2,
即a2+a4=a4+a6=…=2,
∴S60=(a1+a3+…+a59)+(a2+a4+…+a60)
=(1+3+…)+(2+2+…)
=30×1+
| 30×29 |
| 2 |
故答案为:930.
点评:本题考查数列的前60项和的求法,是中档题,解题时要注意分类讨论思想和分组求和法的合理运用.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
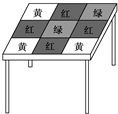 一张方桌的图案如图所示,将一颗豆子随机地扔到桌面上,假设豆子不落在线上,下列事件的概率
一张方桌的图案如图所示,将一颗豆子随机地扔到桌面上,假设豆子不落在线上,下列事件的概率(1)豆子落在红色区域概率为
| 4 |
| 9 |
(2)豆子落在黄色区域概率为
| 1 |
| 3 |
(3)豆子落在绿色区域概率为
| 2 |
| 9 |
(4)豆子落在红色或绿色区域概率为
| 1 |
| 3 |
(5)豆子落在黄色或绿色区域概率为
| 4 |
| 9 |
其中正确的结论有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
已知x,y满足约束条件
,则目标函数z=2x-3y的最大值( )
|
| A、2 | B、3 | C、4 | D、5 |
若z=
,则复数z的虚部为( )
| 2-i |
| 1+2i |
| A、i | B、-i | C、1 | D、-1 |
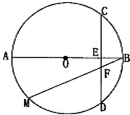 如图,AB为半径为2的圆O的直径,CD为垂直于AB的一条弦,垂足为E,弦BM与CD交于点F.则AC2+BF•BM=
如图,AB为半径为2的圆O的直径,CD为垂直于AB的一条弦,垂足为E,弦BM与CD交于点F.则AC2+BF•BM= 某校高三第一次模考中,对总分450分(含450分)以上的成绩进行统计,其频率分布直方图如图所示,若650~700分数段的人数为90,则500~550分数段的人数为
某校高三第一次模考中,对总分450分(含450分)以上的成绩进行统计,其频率分布直方图如图所示,若650~700分数段的人数为90,则500~550分数段的人数为