题目内容
设x、y满足约束条件
,若x2+y2≥a恒成立,则实数a的最大值为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,设z=x2+y2,利用z的几何意义,求出z的最小值,即可得到结论.
解答:
解:作出不等式组对应的平面区域如图:
设z=x2+y2,则z的几何意义为区域内的点P(x,y)到原点O距离平方的取值范围,
由图象可知z的最小值为圆心O到直线x+y=1的距离的平方,
∵d=
,
∴z≥d2=
,
要使x2+y2≥a恒成立,则a≤
,
即实数a的最大值为
,
故选:A.

设z=x2+y2,则z的几何意义为区域内的点P(x,y)到原点O距离平方的取值范围,
由图象可知z的最小值为圆心O到直线x+y=1的距离的平方,
∵d=
| 1 | ||
|
∴z≥d2=
| 1 |
| 2 |
要使x2+y2≥a恒成立,则a≤
| 1 |
| 2 |
即实数a的最大值为
| 1 |
| 2 |
故选:A.
点评:本题主要考查线性规划的应用,根据条件设z=x2+y2,利用z的几何意义即可求出a的取值范围.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
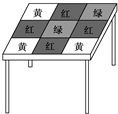 一张方桌的图案如图所示,将一颗豆子随机地扔到桌面上,假设豆子不落在线上,下列事件的概率
一张方桌的图案如图所示,将一颗豆子随机地扔到桌面上,假设豆子不落在线上,下列事件的概率(1)豆子落在红色区域概率为
| 4 |
| 9 |
(2)豆子落在黄色区域概率为
| 1 |
| 3 |
(3)豆子落在绿色区域概率为
| 2 |
| 9 |
(4)豆子落在红色或绿色区域概率为
| 1 |
| 3 |
(5)豆子落在黄色或绿色区域概率为
| 4 |
| 9 |
其中正确的结论有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
已知数列{an}是等差数列,a1=tan225°,a5=13a1,设Sn为数列{(-1)nan}的前n项和,则S2014=( )
| A、2014 | B、-2014 |
| C、3021 | D、-3021 |
已知x,y满足约束条件
,则目标函数z=2x-3y的最大值( )
|
| A、2 | B、3 | C、4 | D、5 |
已知a,b,c∈R,下列四个命题:
(1)若a>b 则ac2>bc2
(2)若
>
则a>b
(3)若a>b则a2>b2
(4)若a>b则
>
其中正确的个数是( )
(1)若a>b 则ac2>bc2
(2)若
| a |
| c |
| b |
| c |
(3)若a>b则a2>b2
(4)若a>b则
| 1 |
| b |
| 1 |
| a |
其中正确的个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
双曲线2x2-y2=-1的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|