题目内容
下列说法中正确的有
①平均数不受少数几个极端值的影响,中位数受样本中的每一个数据影响.
②抛掷两枚硬币,出现“两枚都是正面朝上”、“两枚都是反面朝上”、“恰好一枚硬币正面朝上”的概率一样大.
③用样本的频率分布估计总体分布的过程中,样本容量越大,估计越准确.
④一组数据的方差越大,说明这组数据的波动越大.
⑤向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是古典概型.
①平均数不受少数几个极端值的影响,中位数受样本中的每一个数据影响.
②抛掷两枚硬币,出现“两枚都是正面朝上”、“两枚都是反面朝上”、“恰好一枚硬币正面朝上”的概率一样大.
③用样本的频率分布估计总体分布的过程中,样本容量越大,估计越准确.
④一组数据的方差越大,说明这组数据的波动越大.
⑤向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是古典概型.
考点:命题的真假判断与应用
专题:概率与统计
分析:平均数受少数几个极端值的影响,可以判断①是否正确;
求出抛掷两枚硬币,出现“两枚都是正面朝上”的概率、“两枚都是反面朝上”的概率和“恰好一枚硬币正面朝上”的概率,可判断②是否正确;
根据用样本的频率分布估计总体分布的过程中,样本容量与估计是否准确的关系,判断③是否正确;
根据方差是描述数据的波动大小的量,可以判定④是否正确;
根据古典概型与几何概型的区别,可以判定⑤是否正确.
求出抛掷两枚硬币,出现“两枚都是正面朝上”的概率、“两枚都是反面朝上”的概率和“恰好一枚硬币正面朝上”的概率,可判断②是否正确;
根据用样本的频率分布估计总体分布的过程中,样本容量与估计是否准确的关系,判断③是否正确;
根据方差是描述数据的波动大小的量,可以判定④是否正确;
根据古典概型与几何概型的区别,可以判定⑤是否正确.
解答:
解:①∵平均数受少数几个极端值的影响,中位数也受样本中的每一个数据影响,∴命题是错误的;
②抛掷两枚硬币,出现“两枚都是正面朝上”的概率为
、“两枚都是反面朝上”的概率为
、“恰好一枚硬币正面朝上”的概率为
,
它们的概率不一样大,∴命题错误;
③用样本的频率分布估计总体分布的过程中,样本的容量越大,估计越准确,是正确的,通常取样本时,容量尽可能大一些;
④方差是描述数据的波动大小的量,∴一组数据的方差越大,这组数据的波动越大,命题正确;
⑤向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是几何概型,不是古典概型,∴命题错误;
所以,以上正确的命题是③④;
故答案为:③④.
②抛掷两枚硬币,出现“两枚都是正面朝上”的概率为
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
它们的概率不一样大,∴命题错误;
③用样本的频率分布估计总体分布的过程中,样本的容量越大,估计越准确,是正确的,通常取样本时,容量尽可能大一些;
④方差是描述数据的波动大小的量,∴一组数据的方差越大,这组数据的波动越大,命题正确;
⑤向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是几何概型,不是古典概型,∴命题错误;
所以,以上正确的命题是③④;
故答案为:③④.
点评:本题考查了有关概率与统计的命题真假的判定问题,是基础题.

练习册系列答案
相关题目
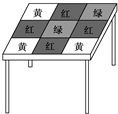 一张方桌的图案如图所示,将一颗豆子随机地扔到桌面上,假设豆子不落在线上,下列事件的概率
一张方桌的图案如图所示,将一颗豆子随机地扔到桌面上,假设豆子不落在线上,下列事件的概率(1)豆子落在红色区域概率为
| 4 |
| 9 |
(2)豆子落在黄色区域概率为
| 1 |
| 3 |
(3)豆子落在绿色区域概率为
| 2 |
| 9 |
(4)豆子落在红色或绿色区域概率为
| 1 |
| 3 |
(5)豆子落在黄色或绿色区域概率为
| 4 |
| 9 |
其中正确的结论有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
双曲线2x2-y2=-1的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
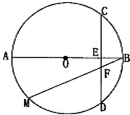 如图,AB为半径为2的圆O的直径,CD为垂直于AB的一条弦,垂足为E,弦BM与CD交于点F.则AC2+BF•BM=
如图,AB为半径为2的圆O的直径,CD为垂直于AB的一条弦,垂足为E,弦BM与CD交于点F.则AC2+BF•BM= 某校高三第一次模考中,对总分450分(含450分)以上的成绩进行统计,其频率分布直方图如图所示,若650~700分数段的人数为90,则500~550分数段的人数为
某校高三第一次模考中,对总分450分(含450分)以上的成绩进行统计,其频率分布直方图如图所示,若650~700分数段的人数为90,则500~550分数段的人数为