题目内容
20.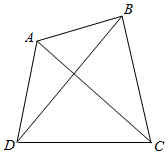 为了测量河对岸两点A,B之间的距离,在河岸的这边选取点C、D,测得∠ADC=75°,∠BDC=60°,∠ACD=45°,∠BCD=75°,CD=20$\sqrt{3}$m,设A,B,C,D在同一平面内,求A,B之间的距离.
为了测量河对岸两点A,B之间的距离,在河岸的这边选取点C、D,测得∠ADC=75°,∠BDC=60°,∠ACD=45°,∠BCD=75°,CD=20$\sqrt{3}$m,设A,B,C,D在同一平面内,求A,B之间的距离.
分析 在△BCD中使用正弦定理解出BC,在△ACD中使用正弦定理解出AC,在△ABC中使用余弦定理解出AB.
解答 解:在△BCD中,∠CBD=180°-∠BDC-∠BCD=45°,
由正弦定理得$\frac{CD}{sin∠CBD}=\frac{BC}{sin∠BDC}$,即$\frac{20\sqrt{3}}{\frac{\sqrt{2}}{2}}=\frac{BC}{\frac{\sqrt{3}}{2}}$,解得BC=30$\sqrt{2}$m.
在△ACD中,∠CAD=180°-∠ADC-∠ACD=60°.
由正弦定理得$\frac{CD}{sin∠CAD}=\frac{AC}{sin∠ADC}$,即$\frac{20\sqrt{3}}{\frac{\sqrt{3}}{2}}=\frac{AC}{\frac{\sqrt{6}+\sqrt{2}}{4}}$,解得AC=10$\sqrt{6}$+10$\sqrt{2}$m.
在△ABC中,∠ACB=∠BCD-∠ACD=30°,
由余弦定理得AB2=AC2+BC2-2AC×BC×cos∠ACB=800-200$\sqrt{3}$.
∴AB=10$\sqrt{8-2\sqrt{3}}$m.
点评 本题考查了正余弦定理在解三角形中的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.$\frac{i-1}{1+i}$=( )
| A. | -i | B. | i | C. | 1+i | D. | 1-i |
9.若cos2x=$\frac{1}{2}$,其中$\frac{π}{2}$<x<π,则x的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{3}$ |