题目内容
12.已知$f(α)=\frac{sin(π-α)cos(2π-α)tan(-α+π)}{tan(-π-α)sin(-π-α)}$(Ⅰ)化简f(α);
(Ⅱ)若α是第三象限角,且cos($α-\frac{3π}{2}$)=$\frac{{2\sqrt{6}}}{5}$,求f(α)的值.
分析 (Ⅰ)由已知利用诱导公式能求出f(α)=cosα.
(Ⅱ)由α为第三象限角,利用诱导公式能求出sinα,再由同角三角函数关系式能求出f(α)的值.
解答 解:(Ⅰ)$f(α)=\frac{sin(π-α)cos(2π-α)tan(-α+π)}{tan(-α-π)sin(-π-α)}=\frac{sinαcosα(-tanα)}{-tanαsinα}=cosα$.(5分)
(Ⅱ)∵α为第三象限角,且$cos(α-\frac{3π}{2})=-sinα=\frac{{2\sqrt{6}}}{5}$,(7分)
$\begin{array}{l}∴sinα=-\frac{{2\sqrt{6}}}{5}\\∴cosα=-\sqrt{1-{{sin}^2}α}=-\frac{1}{5}\end{array}$.
∴$f(α)=cosα=-\frac{1}{5}$.(10分)
点评 本题考查三角函数化简求值,是基础题,解题时要认真审题,注意诱导公式的合理运用.

练习册系列答案
相关题目
2.“吸烟有害健康,吸烟会对身体造成伤害”,哈尔滨市于2012年5月31日规定室内场所禁止吸烟.美国癌症协会研究表明,开始吸烟年龄(X)分别为16岁、18岁、20岁和22岁,其得肺癌的相对危险度(Y)依次为15.10、12.81、9.72、3.21;每天吸烟(U)10支、20支、30支者,其得肺癌的相对危险度(v)分别为7.5、9.5和16.6.用r1表示变量X与y之间的线性相关系数,用r2表示变量U与V之间的线性相关系数,则下列说法正确的是( )
| A. | rl=r2 | B. | r1>r2>0 | C. | 0<r1<r2 | D. | r1<0<r2 |
3.已知函数f(x)=sin(2ωx一$\frac{π}{4}$)(ω>0)的最小正周期为π,则函数f(x)的图象( )
| A. | 关于点($\frac{π}{8}$,0)对称 | B. | 关于直线x=$\frac{π}{8}$对称 | ||
| C. | 关于点(-$\frac{π}{4}$,0)对称 | D. | 关于直线x=-$\frac{π}{4}$对称 |
4.已知集合A={x|x<-2},B={x|x2>4},则“x∈A”是“x∈B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.已知i是虚数单位,若复数z满足z=$\frac{{i}^{3}}{1+i}$,则z为( )
| A. | $\frac{1+i}{2}$ | B. | $\frac{1-i}{2}$ | C. | $\frac{-1-i}{2}$ | D. | $\frac{-1+i}{2}$ |
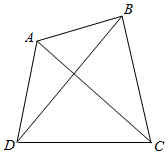 为了测量河对岸两点A,B之间的距离,在河岸的这边选取点C、D,测得∠ADC=75°,∠BDC=60°,∠ACD=45°,∠BCD=75°,CD=20$\sqrt{3}$m,设A,B,C,D在同一平面内,求A,B之间的距离.
为了测量河对岸两点A,B之间的距离,在河岸的这边选取点C、D,测得∠ADC=75°,∠BDC=60°,∠ACD=45°,∠BCD=75°,CD=20$\sqrt{3}$m,设A,B,C,D在同一平面内,求A,B之间的距离.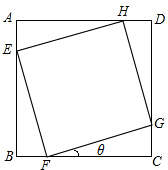 如图所示,某住宅小区内有一正方形草地ABCD,现欲在其中修建一个正方形花坛EFGH,若已知花坛面积为正方形草地面积的$\frac{2}{3}$,则θ=arctan(2-$\sqrt{3}$).
如图所示,某住宅小区内有一正方形草地ABCD,现欲在其中修建一个正方形花坛EFGH,若已知花坛面积为正方形草地面积的$\frac{2}{3}$,则θ=arctan(2-$\sqrt{3}$).