题目内容
9.若cos2x=$\frac{1}{2}$,其中$\frac{π}{2}$<x<π,则x的值为( )| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{3}$ |
分析 根据x的取值范围,利用cos2x=$\frac{1}{2}$,判断2x的取值范围,从而求出x的值.
解答 解:∵$\frac{π}{2}$<x<π,∴π<2x<2π,
又cos2x=$\frac{1}{2}$,
∴$\frac{3π}{2}$<2x<2π,
∴2x=$\frac{5π}{3}$,
解得x=$\frac{5π}{6}$.
故选:B.
点评 本题考查了利用三角函数值求对应角的应用问题,解题时应考虑角的取值范围,是基础题目.

练习册系列答案
相关题目
19.已知复数z满足z(1+i)=1(i为虚数单位),则z=( )
| A. | $\frac{1-i}{2}$ | B. | $\frac{1+i}{2}$ | C. | 1-i | D. | 1+i |
4.已知集合A={x|x<-2},B={x|x2>4},则“x∈A”是“x∈B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.函数f(x)=log2(4x+1)的值域为( )
| A. | [0,+∞) | B. | (0,+∞) | C. | [1,+∞) | D. | (1,+∞) |
1.已知i是虚数单位,若复数z满足z=$\frac{{i}^{3}}{1+i}$,则z为( )
| A. | $\frac{1+i}{2}$ | B. | $\frac{1-i}{2}$ | C. | $\frac{-1-i}{2}$ | D. | $\frac{-1+i}{2}$ |
18.若命题:“?x∈R,x2-2ax+a≤0”为假命题,则$\frac{{2{a^2}+1}}{a}$的最小值是( )
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |
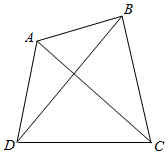 为了测量河对岸两点A,B之间的距离,在河岸的这边选取点C、D,测得∠ADC=75°,∠BDC=60°,∠ACD=45°,∠BCD=75°,CD=20$\sqrt{3}$m,设A,B,C,D在同一平面内,求A,B之间的距离.
为了测量河对岸两点A,B之间的距离,在河岸的这边选取点C、D,测得∠ADC=75°,∠BDC=60°,∠ACD=45°,∠BCD=75°,CD=20$\sqrt{3}$m,设A,B,C,D在同一平面内,求A,B之间的距离.