题目内容
10.(x2+$\frac{1}{{x}^{2}}$-2)n展式中的常数项是70,则n=4.分析 先求出二项式展开式的通项公式,再令x的幂指数等于0,求得n=r,再根据常数项为70,求得n的值.
解答 解:∵(x2+$\frac{1}{{x}^{2}}$-2)n =${(x-\frac{1}{x})}^{2n}$的展式的通项公式为Tr+1=${C}_{2n}^{r}$•(-1)r•x2n-2r,
令2n-2r=0,求得n=r,故展开式的常数项为(-1)n•${C}_{2n}^{n}$=70,
求得n=4,
故答案为:4.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知i是虚数单位,若复数z满足z=$\frac{{i}^{3}}{1+i}$,则z为( )
| A. | $\frac{1+i}{2}$ | B. | $\frac{1-i}{2}$ | C. | $\frac{-1-i}{2}$ | D. | $\frac{-1+i}{2}$ |
18.若命题:“?x∈R,x2-2ax+a≤0”为假命题,则$\frac{{2{a^2}+1}}{a}$的最小值是( )
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |
15.设i为虚数单位,则i2014=( )
| A. | 1 | B. | i | C. | -1 | D. | -i |
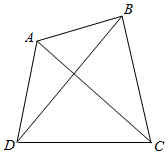 为了测量河对岸两点A,B之间的距离,在河岸的这边选取点C、D,测得∠ADC=75°,∠BDC=60°,∠ACD=45°,∠BCD=75°,CD=20$\sqrt{3}$m,设A,B,C,D在同一平面内,求A,B之间的距离.
为了测量河对岸两点A,B之间的距离,在河岸的这边选取点C、D,测得∠ADC=75°,∠BDC=60°,∠ACD=45°,∠BCD=75°,CD=20$\sqrt{3}$m,设A,B,C,D在同一平面内,求A,B之间的距离.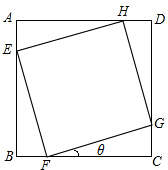 如图所示,某住宅小区内有一正方形草地ABCD,现欲在其中修建一个正方形花坛EFGH,若已知花坛面积为正方形草地面积的$\frac{2}{3}$,则θ=arctan(2-$\sqrt{3}$).
如图所示,某住宅小区内有一正方形草地ABCD,现欲在其中修建一个正方形花坛EFGH,若已知花坛面积为正方形草地面积的$\frac{2}{3}$,则θ=arctan(2-$\sqrt{3}$).